Some of you may recall my complaining about the lack of USB oscilloscopes for the Mac a couple of years ago, when I bought myself a used Kikusui COS5060 analog oscilloscope.  In the comments for my complaint post, someone named Chris had recommended last March that I check out bitscope.com, as they supposedly had software for the Mac OS X.

This year for my birthday, I bought myself the Bitscope Pocket Analyzer, a tiny (6.6 × 6.2 × 1.7 cm) USB attachment that can act as a 2-channel oscilloscope, plus a few digital channels, plus a waveform generator. The price is a little high (about $300) and it was a hassle to buy, because my credit card company was convinced that a transaction from Australia had to be fraudulent, and didn’t get around to checking with me for a couple of days, after rejecting the purchase three times.  Luckily the bitscope people were very nice about it and even gave me free faster shipping, which was very generous, as none of the delays had anything to do with them—just with my miserable excuse for a bank (I’m looking at you, Wells Fargo!).

The bitscope does have software for the Mac OS X, which is appropriately labeled as beta-release software.  There are still bugs in it (for example, when I try to save a screen shot in jpg format, it saves it in png format instead), but most of the functionality one would want is there. Saving also only saves the main scope display, not all the setting displays around it (so there is no record made of most of the settings, and any cursor readings have to be manually recorded, or you use the screen-shot features of your operating system).  The value displayed on the screenshot that is saved is the “bias” or mean waveform voltage—perhaps the most useless of the measurements they could have chosen to make the displayed one. There are probably other bugs, but I’m still unfamiliar enough with the controls that I usually can’t tell when I’m making a mistake vs. when the software is.

Like other digital scopes, the Bitscope records a full frame before displaying anything, and it alternates a frame of channel A with a frame of channel B.  This can be rather disconcerting if you are using a slow time base (like for an EKG signal), as nothing appears on the screen for a few seconds after the trigger.  With higher speed time bases, the frame rate is fast enough that the delay is not noticeable.

Also like other digital scopes, the controls are highly idiosyncratic and difficult to learn.  In the case of the bitscope software, the controls are even more idiosyncratic than usual—they have something they call “Act on Touch” controls, which behave differently depending where on the button you click:

click and drag up and down or left and right on a parameter to adjust its value. Click on the left or right edge of the parameter to select a previous or next value.

Right-click (or control-click on a Mac or press-and-hold on a tablet) to pop up a context menu and double-click to open an editor to type in a value or select a default value.

Note that the cursors cannot be adjusted by this “Act on Touch” method nor with the arrow keys, but can only be dragged on the image, which makes measuring some parameters more difficult that in needs to be.

I did eventually manage to do some plots that correspond to the taking the thresholds of a pMOS field-effect transistor (pFET) and an nMOS field-effect transistor (nFET).

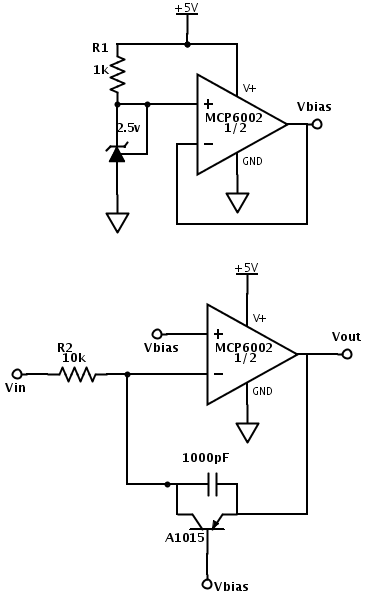
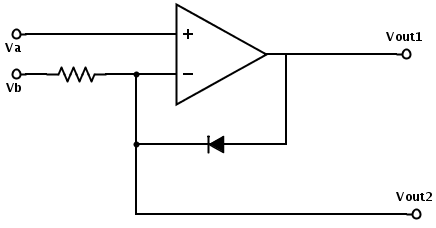
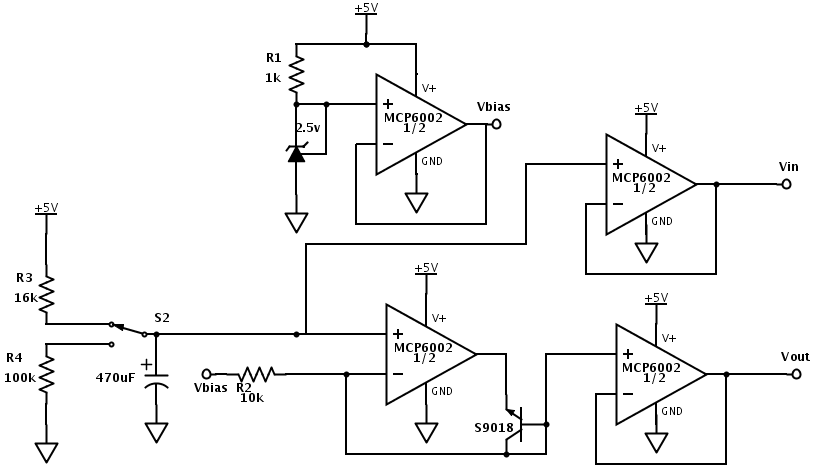
Test circuits for determining thresholds of the FET transistors. I only hooked up one of the test circuits at a time (nFET or pFET), not both at once.

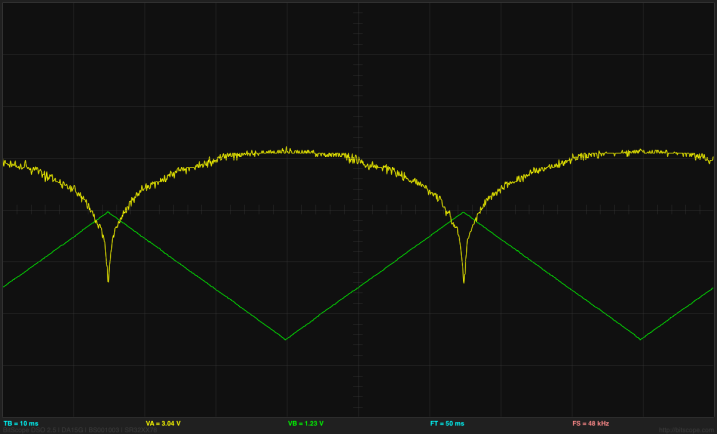
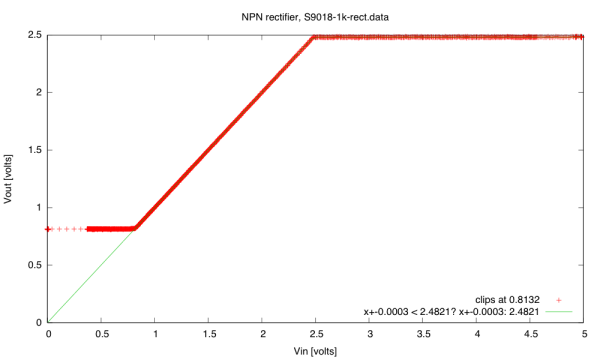
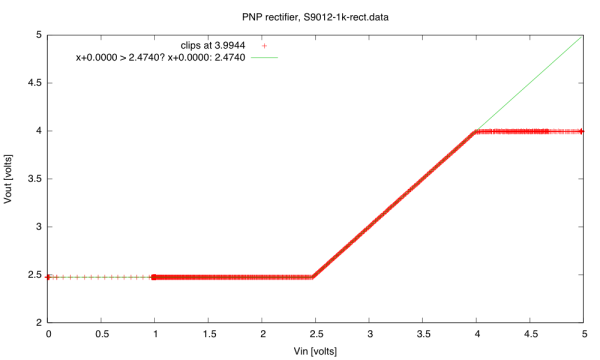
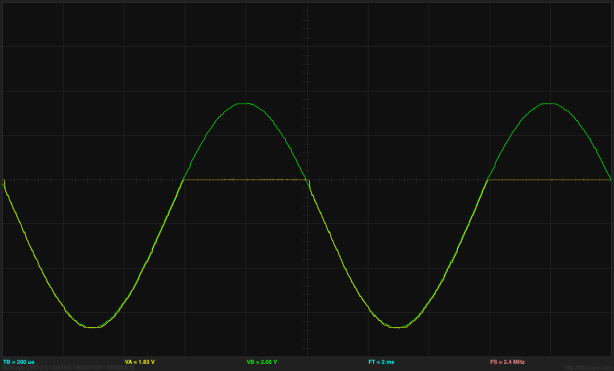
Results for testing the NTD2955 pMOS FET. I set the cursor about where the transistor turns on, at 2.08V, which gives a threshold voltage of 2.08V-4.93V= -2.85V, close to the nominal -2.80V, and well within the specs (-2.0V to -4.0V).
I see that I ended up with non-standard vertical scaling here for channel A (the Vp voltage).  Changing the range of the inputs picks non-standard scaling by default (another stupid choice by the software designers).

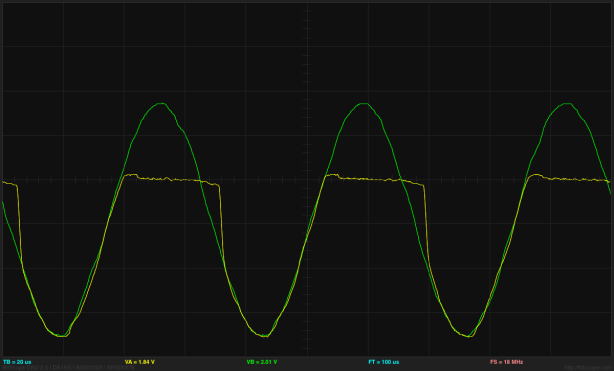
The curve clearly shows the quadratic dependency of the current on the gate voltage above threshold.  With a little more care in using the bitscope, I can see that I get 1v (100mA) when the voltage is 1.56v (so -3.37 relative to the source), which would give me something like I= 370(2.85V+V_DS)² mA/V².

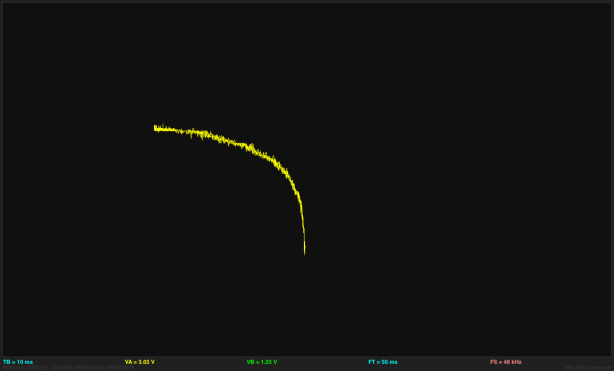
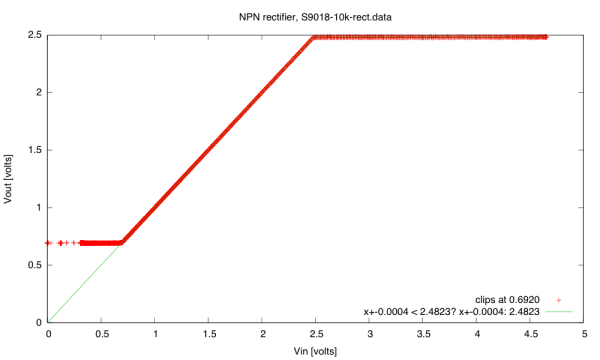
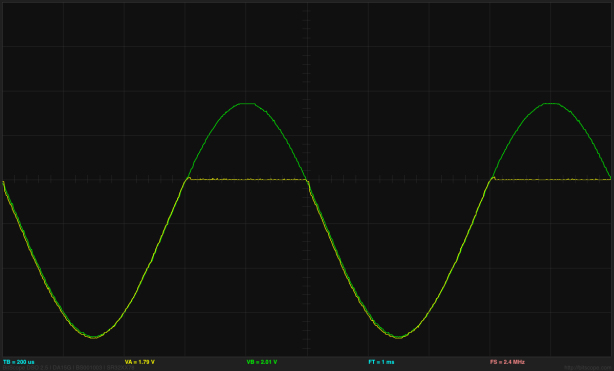
I also did a similar plot for an nMOS FET:

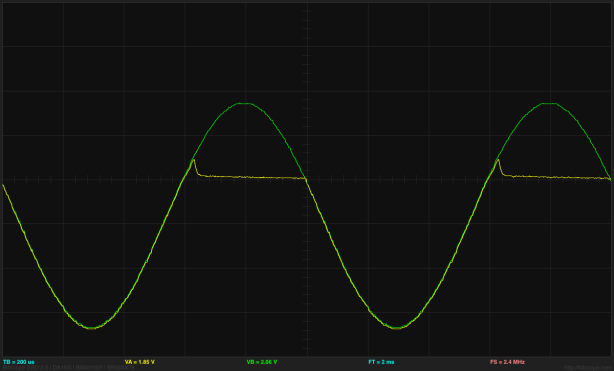
Bogus threshold plot for NTD5867 nMOS FET.   The current does not seem to follow a quadratic curve above the threshold voltage, because the 5.2V range on Channel A is truncating part of the curve (which goes from -2.6V to +2.6V, not 0V to 5.2V).

The current for the nFET peaked at almost 500mA, which is a 2.5W power dissipation: far more than the lowly ¼W resistor could handle even for a short duty cycle. I had to pull the power wire from the breadboard quickly after each test, to keep from burning up the resistor. I did not repeat this test with a 10Ω resistor, but switched to a 100Ω resistor for safety. If I have the students measure the thresholds for their FETs, I’ll have to make sure they compute the minimum resistance value that they can safely use with the voltage they are testing at, and not just blindly grab a convenient size that was sitting around on the benchtop, as I did.

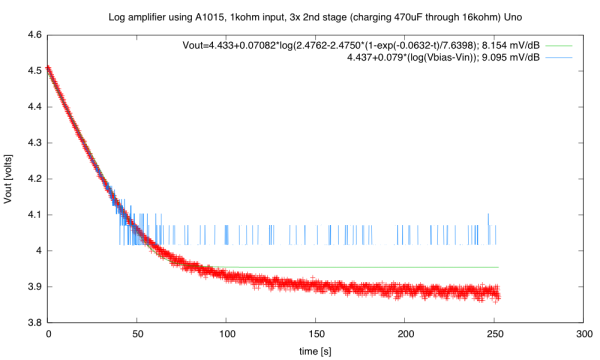
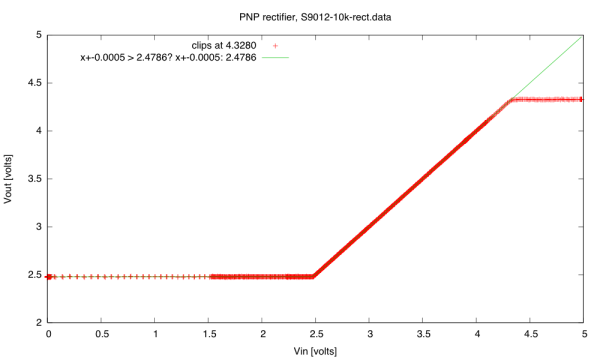
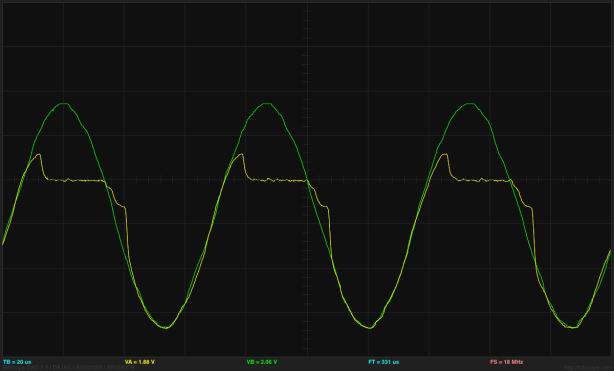
With a 100Ω series resistor, I detect the nFET turning on at 1.66V, and see the expected quadratic dependence of the saturation current on gate voltage above threshold.  The 1.66V is not close to the nominal 1.8V threshold, but is within specs (between 1.5V and 2.5V).

The 100Ω resistor does not get warm, as the 0.25W max power dissipation times the approximately 1/3 duty cycle is well within the ¼W power limit.  Using a larger resistor makes the threshold detection a little easier, since turning the transistor on only a little to get 1mA of current, provides an easily seen 0.1v swing.

At a gate voltage of 2.08V (0.42V above threshold), the output current is 40mA, so the saturation current is about 227(V_DS-1.66V)² mA/V².

Now that I’ve characterized the FETs, I should probably try designing a power amp using them. I tried several designs this morning in CircuitLab, but the circuit lab simulator has serious problems with op amp circuits. It gets confused by the feedback loops and neglects to bound the voltage values, so I was getting DC “solutions” with outputs in the teravolts. It would be quite a trick to get a teravolt output from an op amp with a 5v power supply!

Some of my designs were quite clever—one that I was curious about used DC coupling throughout, but automatically compensated for the DC offset of the microphone and should keep the voltage across the speaker centered without needing a dual-rail supply (that is, no high-current center supply) nor large DC-blocking capacitors. It took 4 op amps and a differential amp, though, so was not a cheap solution (if it even works—I’ll have to wire it up to find out, as the simulator couldn’t handle it).

I think I’d better try a couple of straight-forward designs and see how they work, first—designs the students are more likely to come up with.

In More mess in the FET modeling lab, I reported observing an S-type negative resistance in the nFET that I had not expected:

Negative resistance 12mA and 50mA. (click to enlarge)

I decided to see if the negative resistance was really there and usable by making a negative resistance oscillator. The usual such oscillator for a negative resistance is a loop containing an inductor, a capacitor, and the negative resistance. Because I wanted an audio frequency oscillator, I needed a fairly large inductor (the angular frequency is ). However, I am also constrained by the resistance of the inductor, since the sum of the resistance around the loop has to remain negative. Estimating the negative resistance by fitting a straight-line to the appropriate part of the V-vs-I curve gave me a negative resistance of –2.145Ω. So the inductor needs a DC resistance under 2Ω.

Inductors are not something I have many of, but I looked through my parts drawers for any I might have gotten years ago in surplus grab-bag of parts. I found some tiny transformers with unknown specifications, so I tried measuring one to see if it had a high enough inductance with a low enough resistance. Transformers seemed more promising to me than simple coils of wire, because they are likely to have a ferrite core to increase the inductance without increasing the resistance, and the secondary coil gives another possibility for resonance.

I measured the DC resistance of the transformer and found that the tapped coil has a resistance of about 106Ω and the untapped coil about 0.1Ω (but my meter is not too good at resistances less than 1Ω). I then tried measuring the inductance using the same techniques I used for characterizing loudspeakers and electrodes (see Better measurement of conductivity of saline solution or Characterizing tactile transducer again), making a number of measurements of RMS voltage across the device and across a series resistor at different frequencies, then fitting a model.  Since I was looking mainly for the inductance in a simple R+L series model, I mainly looked at higher frequencies.  For the tapped coil, I got R=107.2Ω, L = 0.0226H, and for the untapped coil I got  R<0.1Ω and  L=6.76µH (I hadn’t gone to low enough frequencies to estimate R well, and I didn’t really care, since it was much less than 2Ω).

I tried the tapped coil first, but as expected from the resistance, could not get an oscillation.  I then tried the untapped coil with an electrolytic capacitor, and still couldn’t get an oscillation.  Finally, I tried the untapped coil with a 4.7µF ceramic capacitor and got an oscillation around 29.9kHz with a bias current around 21mA.  The waveform was not pretty:

Waveform of the negative resistance oscillator with no load on the secondary of the transformer. Bias is about 21mA. Note, the oscilloscope is connected across the secondary coil of the transformer, which appears to have around 3300 times as many turns as the primary, making the voltage larger and easier to observe with the BitScope USB oscilloscope.

I tried cleaning up the waveform by adding a capacitor across the secondary coil of the transformer. Too large a capacitance killed the oscillation and too small a capacitance did little to clean up the signal. I got the best results with a 680pF capacitor:

Waveform with a 680pF capacitor loading the secondary coil of the transformer.

Here then is the final circuit:

Negative resistance oscillator using the unexpected S-type negative resistance of the NTD5867 nFET. Biasing the diode-connected nFET around 21mA produced oscillations.

This is not a particularly practical circuit, as 21mA is a lot of current to get rather feeble, noisy oscillations, but it does show that the negative resistance I observed is a real phenomenon, and not an artifact of sloppy measuring on my part (as I had first feared). I wonder whether the negative resistance when switching from subthreshold to above-threshold conduction is a common property of diode-connected power FETs (or of FETs in general), or whether it is something specific to this part. I’ve never heard of it before, but I only used FETs in nMOS and cMOS digital VLSI design, where simple models sufficed—no one bothered to teach me anything about how FETs behave in this region.

For those interested in the spectra of the oscillations, I took screen grabs of Bitscope’s spectrum analysis. Unfortunately, the cursor obscures the fundamental peak—there doesn’t seem to be any way to see the peak and display the frequency at the same time. (I also hate the black-background display, which is only there because scopes have “always” had dark backgrounds—they are no longer a necessary evil, just an evil.)

Spectrum without a capacitor on the secondary coil of the transformer.

Spectrum with 680pF on secondary coil of transformer.

In today’s class I had originally planned to cover the following topics:

• RMS voltage. I keep putting off a discussion of the 3 different systems for reporting AC voltage (amplitude, peak-to-peak, and RMS), so I’d better start with it.
• hysteresis.  I have a pretty decent writeup (I think) in the lab handout, but I’m going to have to step the students through it, because I’m not sure that all of them learn well from reading.
• hysteresis oscillator. Yet another time to talk about RC time constants.  The problem here is going to be that there is a somewhat arbitrary scaling of the RC time constant based on what the threshold voltages are.

After last night’s late-night blog post, I decided to add a few minutes at the beginning of the class talking about the “comfort zone” and the “zone of proximal growth”, and how it was ok (even good) to be uncomfortable, but that I was trying to hit the sweet spot of maximizing learning for them without good feedback on when I had hit it.  There were likely to be times when I went too fast or too far, and took them into the range of “impossible”, where they either shut down or ran around in mental circles without getting there.  I pointed out that I was out of my comfort zone in teaching this class, and learning a lot about how to teach the subject, since the class was not quite like any of my previous courses, which had either involved students who had already started “thinking like engineers” or for which that was not a major goal.

As it turned out, there was a natural segue to this topic, as several students complained about how much time they were spending struggling with gnuplot.  They were reporting times in excess of 12 hours on gnuplot, when I had expected the plots for last week’s lab to take them only an hour.  They reported having more trouble using gnuplot than with the circuits concepts and electrochemistry that the lab was supposed to be helping them learn. I believe that learning to use a plotting and model-fitting tool will be very useful for them no matter what branch of bioengineering they end up working in.

I don’t think that the problems they were having are unique to gnuplot and changing tools is not likely to help—in fact, gnuplot has one of the simplest interfaces of tools that can fit multiple parameters for complicated functions. I’m not sure, however, where the conceptual difficulty is for them, and so I asked if one or two of the ones who were having the most difficulty could sit down with me and show me where they were getting stuck (after lab tomorrow, on Friday, or after class on Monday).  Perhaps by watching them work, I can get a better idea where the difficulty is and devise a lesson, handout, or other intervention to get them unstuck.  I also offered one-on-one tutoring to them (again after lab or in Monday’s office hours), but until I know what the sticking point is, my tutoring is likely to be pseudoteaching again, where I guide them through the process and we’re all convinced they’ve got it, but when they try a real problem on their own, they still get stuck.

Not everyone who was introduced to gnuplot is having this difficulty (a few students have reported to me that they are now applying gnuplot for their senior theses), but enough were having trouble that I certainly can’t dismiss the problem as irrelevant nor can I expect the students to tutor each other (an intervention that works well when most of the class understands the concepts, since explaining to the few who need help can help people clarify their own understanding).

The circuits topics that I wanted to teach went well.

I introduced RMS voltage as the DC voltage that provides the same average power as the AC signal of a given amplitude, and we did the definite integral for computing the average power.  (I gave them trig formula , and reassured them that I did not expect them to remember trigonometry—this may be the only place this quarter where we use a trig identity.)  I also had them derive the RMS voltage for a square wave, so they could see that the ratio was a special case for sine waves and not a general phenomenon.

I then covered digital amplifiers and hysteresis, using the figures from the lab handout.  I think I got across the idea of hysteresis using the figures and  the example of a thermostat and furnace that you don’t want to cycle on and off a lot. It’s hard to tell whether they’ve really gotten the idea or not, though, and I don’t know how to check other than by seeing what they write in their lab reports.

The relaxation oscillator was not as thoroughly covered.  We stepped through the charging and discharging of the capacitor, but did not derive formulas for how long it takes to charge and discharge, as a function of R, C, the two threshold voltages, and the two output voltages.  We did wave our hands at the idea that all the times are proportional to the RC time constant, but did not attempt to determine what the proportionality constant is.  I suggested that they determine it empirically in the lab, rather than deriving the formula, since I’m not confident that they could derive the constants, given that the input voltage is decaying exponentially towards the output voltage.  The math seems simple to me, but explaining it to them would take more time than we had in class today, and I’m not sure how much they would retain of it.  I’m hoping that some of the more diligent students will attempt the derivation on their own, as it provides another concrete use for the formula.  I suspect that most of them can handle the algebra for the exponential decay towards 0V, but that they will have trouble with expressing the exponential decay towards 4V (the output high voltage).

I did demo the relaxation oscillator, using the same PC board that they’ll be soldering and displaying the output waveform with the BitScope USB oscilloscope I bought.  I had to power the Arduino board and the oscillator with a separate power supply, since my trials ahead of time showed me that the BitsSope could not display the signal if I powered the Arduino from the laptop.  I think that the problem has to do with the difference between the BitScope ground and the USB ground that is shared with the Arduino—I’ve not yet tried to track it down.  But with a separate power supply everything worked ok.  The projection of the BitScope oscilloscope display worked ok (despite their projection-unfriendly insistence on a black background), and I hope to be able to use it again in a later class.  It is a bit of a pain to set up before class, though, so I’ll want to use it only when the live demo is worth the time and the risk of equipment failure.

This post summarizes my inductance measurements, some of which I did with my son, some independently.

The goal was to determine the inductance of the large inductor that my wife found lying in the street and that I’ve used for a few things in the physics class with my son (like the Speed of sound lab).

Our first measurement used the Arduino data logger to measure an L/R time constant. Using a Schmitt trigger to clean up a mechanical switch output, we measured the voltage across a series resistor (hence the current) for step inputs (both upward and downward).  The upward steps were not useful, as internal resistance of the Schmitt-trigger inverter meant that the step was not clean—the voltage drooped as the current went up. The downward step did not have this problem. The inductance and resistance of the coil were determined by making measurements with both a 10Ω and a 100Ω external resistor, and fitting exponential time constants to the downward steps.  This gave a pair of linear equations in L and R to solve: and .  From these equations I got estimates of 78.5Ω and 0.410H. Note that the resistance includes all the wiring resistance, which was substantial, as I was using flexible jumper wires that are not made from copper and have a high resistance.

The next successful measurement again used a series connection of the unknown inductor and a 100Ω resistor, but the stimulus was a sine wave, rather than a step.  I measured the RMS voltage across the resistor and across the inductor for several different frequencies, and fit an L+R model to the magnitude of the impedance as a function of frequency: .  With this method, I measured the inductance and resistance as 0.369H and 73Ω.  I also tested an AIUR-06-221 inductor (nominally 220µH and 0.252Ω) with a 1Ω current-measuring resistor and got 229µH and 0.258Ω.

Once I finally figured out that DC bias changes capacitance of ceramic capacitors enormously, I managed to get a Colpitts oscillator to work. I should be able to use the frequencies of oscillation with the small inductor and with the large inductor to get an estimate of the inductance of the large inductor.  With the center of the Colpitts tank at virtual ground, the AIUR-06-221 inductor oscillates at 7691Hz and the large one at 180.04 Hz  (both after a few minutes of warmup, as the frequency changes initially).  The ratio of the inductances should be the square of the ratio of the frequencies, that is , or 0.418H, if we use 229µH as the inductance of the AIUR-06-221. Note that this measurement depends on knowing the inductance of the small inductor, but does not require knowing the capacitance of the ceramic capacitors—just that the capacitance is the same for either inductor.

These oscillator measurements and the step-response measurements are consistent, but the modeling of the magnitude of impedance from the voltage measurements at different frequencies seems a bit out of line with them.  The problem may have been that the current-measuring resistor was small, so that the voltage measurements were small.  Perhaps I need another series of measurements with a 10kΩ current-measuring resistor, which should allow a better estimate of L (though not a good estimate of R). I tried again using a 10kΩ resistor and a frequency range from 320Hz to 15kHz, and got a fit for L=0.349H, the lowest estimate so far!

I’m not sure what the problem is with the measurements using the external sine wave.  Perhaps I should do another set using a different function generator, as the Bitscope Pocket analyzer produces pretty bad harmonic distortion at the higher frequencies.  I tried with the Elenco FG-500 function generator (which also has bad harmonic distortion, but different) from about 70Hz to about 16kHz, and got a fit for 0.356H.  This is similar to the measurements I got with the Bitscope function generator.

So, I’m left with a discrepancy that I can’t explain:  measurements of  0.35H for the sine-wave excitation and 0.41H for the L/R step and the Colpitts LC oscillator.

I’ve been thinking of expanding the pressure sensor lab for the Applied Circuits Course to do something more than just measure breath pressure.  Perhaps something that conveys another physics or engineering concept.

One thing I thought of doing was measuring the back pressure and air flow on an aquarium air pump bubbling air into an aquarium. Looking at the tradeoff of flow-rate and back pressure would be a good characterization of an air pump (something I wish was clearly shown in advertisements for aquarium air pumps and air stones).  Measuring flow rate is a bit of a pain—about the best I could think of was to bubble air into an inverted soda bottle (or other known volume) and time it.

This would be a good physics experiment and might even make a decent middle-school product-science science fair project (using a cheap mechanical low-pressure gauge, rather than an electronic pressure sensor), but setting up tanks of water in an electronics lab is a logistic nightmare, and I don’t think I want to go there.

I can generate back pressure with just a simple clamp on the hose, though, and without a flow rate measurement we could do everything completely dry.

Setup for measuring the back pressure for an aquarium air pump (needs USB connection for data logger and power).

Using the Arduino data loggger my son wrote, I recorded the air pressure while adjusting the clamp (to get the y-axis scale correct, I had to use the estimated gain of the amplifier based on resistor sizes used in the amplifier).

The peak pressure, with the clamp sealing the hose shut, seems to be about 14.5 kPa (2.1psi).

I was interested in the fluctuation in the pressure, so I set the clamp to get about half the maximum back pressure, then recorded with the Arduino data logger set to its highest sampling frequency (1ms/sample).

The fluctuation in back pressure seems to have both a 60Hz and a 420Hz component with back pressure at about half maximum.

Because the Arduino data logger has trouble dealing with audio frequency signals, I decided to take another look at the signals using the Bitscope pocket analyzer.

The waveform for the pressure fluctuations from the AQT3001 air pump, with the back pressure about 7.5kPa (half the maximum).

One advantage of using the Bitscope is that it has FFT analysis:

Spectrum for the back pressure fluctuation. One can see many of the multiples of 60Hz, with the particularly strong peak at 420Hz.

I was also interested in testing a Whisper40 air pump (a more powerful, but quieter, pump). When I clamped the hose shut for that air pump, the hi-gain output of the amplifier for the pressure sensor saturated, so I had to use the low gain output to determine the maximum pressure (24.8kPA, or about 3.6psi). The cheap Grafco clamp that I used is a bit hard to get complete shutoff with (I needed to adjust the position of the tubing and use pliers to turn the knob).  It is easy to get complete shutoff if the tube is folded over, but then modulation of less than complete shutoff is difficult.

The fluctuation in pressure shows a different waveform from the AQT3001:

The Whisper40 air pump, with the clamp set to get a bit less than half the maximum back pressure, produces a 60Hz sawtooth pressure waveform, without the strong 420Hz component seen from the AQT3001. The peak-to-peak fluctuation in pressure seems to be largest around this back pressure. The 3kPa fluctuation is larger than for the AQT3001, but the pump seems quieter.

The main noise from the pump is not from the fluctuation in the pressure in the air hose, but radiation from the case of the pump. That noise seems to be least when the back pressure is about 1.1kPa (not at zero, surprisingly). The fluctuation is then all positive pressure, ranging from 0 to 2.2kPa and is nearly sinusoidal, with some 2nd and 3rd harmonic.

As the back pressure increases for the Whisper40, the 2nd, 3rd, and 4th harmonics get larger, but the 60Hz fundamental gets smaller. The 4th harmonic is maximized (with the 1st through 4th harmonics almost equal) at about 22.8kPa, above which all harmonics get smaller, until the air hose is completely pinched off and there is no pressure variation.

When driving the large airstone in our aquarium, the Whisper40 has a back pressure of about 7.50kPa (1.1psi) with a peak-to-peak fluctuation of about 2.6kPa.

I’m not sure whether this air-pump back-pressure experiment is worth adding to the pressure sensor lab.  If I decide to do it, we would need to get a dozen cheap air pumps.  The Tetra 77853 Whisper 40 air pump is $11.83 each from Amazon, but the smaller one for 10-gallon aquariums is only $6.88.  With 12 Ts and 12 clamps, this would cost about $108, which is not a significant cost for the lab.

Yesterday, my son was thinking of adding a microphone to the design he is working on, and was considering adding a fast Fourier transform (FFT) to detect pitch.

He spent a few hours after his 10 a.m.–5 p.m. theater class reading about the FFT algorithm. He found an implementation of the FFT for an Arduino, which he tried reading along with the FFT explanations he found on the web.  I’m actually surprised the the Arduino was capable of doing an FFT, given the slowness of the processor.  It is true that the example code only does a 64-sample FFT with a sampling rate of 1kHz, using 8-bit samples and 16-bit integer arithmetic, but it is reported to do it at better than 10 FFTs per second.

I also pointed him to the Discrete Cosine Transform (DCT), which has somewhat smaller boundary artifacts, and can be computed about twice as fast, but he hasn’t had time to read that yet.  Somewhat surprisingly the DCT article in Wikipedia much better written than the general one on Fourier Transforms, which uses awkward notation and a rather dry, formal factoid dump.

I wanted to show him that FFT did not make pitch extraction trivial (at least not in real musical contexts), so I wired up a microphone and amplifier to my BitScope Pocket Analyzer and we turned on some Internet radio (our local public radio station, KUSP).  The complex mass of rapidly shifting peaks in the FFT made it clear that tracking a pitch would not be easy.  (I think that there are some useful pitch-extraction algorithms that are based on FFT, but they are not trivial.) I think I convinced him that he is better off trying to extract loudness than pitch, if he wants a useful control parameter for his device.

Incidentally, he spent some time yesterday looking for cheap electret microphones. There are quite a few on the market, but many of them say “hand solder only” on the datasheets—even some of the ones with just solder pads! There are mics that can be reflow soldered, but finding prices for them in the 100s is difficult—they mostly seem to be quotes from the manufacturers only. One promising one is the SiSonic SPQ2410HR5H-PD, which is only  3.76mm by 2.24mm and uses a ball grid array (it costs 92¢ in 100s, substantially more than 57¢ for the cheapest through-hole mic (though that needs to be hand soldered). CORRECTION 2013 July 10—that’s a MEMS silicon mic, not an electret.

We looked at digital mics that do the A-to-D conversion already, but the only one with a useful output format was the ADMP441, which costs $4.52 in 100s (way too expensive). The cheaper (down to about $1.02) digital mics all use PDM (pulse-density modulation), but to get that into a usable form inside the ATMega, he’d have to low-pass filter it and pass it through the A/D converter. Still, that may not be any more expensive than an analog mic, DC-blocking high-pass filter, and amplifier, though using a separate amplifier would let him design for the proper microphone sensitivity.  He’s going to have to figure out whether the board area and parts cost are worth the extra functionality of the microphone.  If the board area is not a problem, he could design the mic in, but then have the devices only partially populated to save parts costs, if necessary.

We also noticed that we could tell the bandwidth of the radio station we were listening to, because there was a very clear drop in the spectrum at 10kHz.  I tried capturing that this afternoon, but the station we listened to had a talk program rather than a music program, and I never captured a moment when they were using the full bandwidth.  I tried a different Internet music source, and got the following plot, which seemed to indicate a 12kHz bandwidth, but that may have been limited by the music recording they were playing, rather than the codec used for transmission over the internet.

Snapshot of FFT showing a bandwidth of about 12kHz. The grid for the spectrum is 10dB per division vertically and 6kHz per division horizontally.

Before we’d played with sound input, we’d looked at sine waves generated by the BitScope, by connecting a wire from the GEN output to the CHA input. I don’t think I was able to explain to him why the windowing function used for removing boundary artifacts in the FFT results in spreading the single-frequency spikes into wider peaks. It was too late at night to go into the theory of transforms and how multiplication in the time domain turns into convolution in the frequency domain, and vice versa. For that matter, he hasn’t even had convolution yet, so some of the fundamentals needed for the explanation were missing.

At one point I thought that the FFT on the Bitscope was a crude rectangular window, but I was informed by the Bitscope people that they use a Kaiser window. I should have been able to tell that they were doing some sort of windowing by seeing the spread of the spikes for sine waves, but I wouldn’t have been able to guess which window. (It may be buried in the documentation somewhere.) Actually, now that I look at the spikes, they seem too wide for a Kaiser window, unless they set the α parameter much too large.  They only need the sidelobes to be about 60dB down, which should be a much narrower main lobe—not the 18-bin width I think I’m seeing. Perhaps there is something else spreading the peaks, not just the Kaiser window.

Sine wave and FFT analysis of it (Click on image for larger, clearer picture). Note the harmonic distortion (2nd, 3rd, and 4th harmonic at about –40dB, –45dB, and —53dB).
Good luck figuring out the settings of the Bitscope from the information they show on the display!  TB is the time per division on the x-axis of the plot, while BW=120kHz is the full width of the spectrum (so 12kHz per division), and the sine wave is at about 3kHz.

It is interesting to look a a sine wave that is an exact submultiple of the sampling frequency:

Here is a 2975Hz sine wave, where each period should be 8 samples long. Note the appearance of side bands to either side of the main peak. These artifacts are much smaller if we move to a frequency that does not fit so neatly into the FFT buffer.
Note that the time base is different for this screenshot (20ms/division).

We also looked at the spectra of triangle waves and square waves (since the BitScope waveform generator can do those also). Playing with the duty cycle was fun also. I had not been aware that a duty cycle of 1/n on a square wave or triangle wave suppressed the nth, 2nth, 3nth, … harmonics. I had known that a 50% duty cycle square wave or triangle wave suppressed the even harmonics, but I had never thought about other duty cycles.

Triangle wave with 25% duty cycle, showing suppression of the 4th, 8th, 12th, and 16th harmonics.

My son wanted to design a circuit to convert microphone inputs to loudness measurements usable by an Arduino (or other ATMega processor).  We discussed the idea together, coming up with a few different ideas.

The simplest approach would be to amplify the microphone then do everything digitally on the Arduino. There are several features of this approach:

• The analog circuit is about as simple as we can get: a DC-blocking capacitor and an amplifier.  This would only need one op amp, one capacitor, and 2 resistors (plus something to generate a bias voltage—perhaps another op amp, perhaps a low-drop-out regulator).
• Using digital processing, he can do true RMS voltage computation, and whatever low-pass filtering to smooth the result that he wants.
• He can’t sample very fast on the ATMega processor, so high frequencies would not be handled properly.  He might be able to sample at 9kHz (about as fast as the ADC operates), but that limits him to 4.5kHz. For his application, that might be good enough, so this doesn’t kill the idea.
• He’d like to have a 60dB dynamic range (say from 50dB to 110dB) or more, but the ADC in the ATMega is only a 10-bit converter, so a 60dB range would require the smallest signal to be ±½LSB, which is at the level of the quantization noise.  With careful setting of the gain for the microphone preamp, one might be able to get 55dB dynamic range, but that is pushing it a bit.  The resolution would be very good at maximum amplitude, but very poor for quiet inputs.

Although the mostly digital solution has not been completely ruled out, he wanted to know what was possible with analog circuits.  We looked at two main choices:

• True-RMS converter chips (intended for multimeters).  These do all the analog magic to convert an AC signal to a DC signal with the same RMS voltage.  Unfortunately, they are expensive (over $5 in 100s) and need at least a 5v power supply (he is planning to use all 3.3v devices in his design).  Also true RMS is a bit of overkill for his design, as log(amplitude) would be good enough.
• Using op amps and discrete components to make an amplifier whose output is the logarithm of the amplitude of the input.  Together we came up with the following block diagram:

Block diagram of the loudness circuit. (drawn with SchemeIt).

We then spent some time reading on the web how to make good rectifier circuits and logarithmic amplifiers. I’ll do a post later about the rectifier circuits, since there are many variants, but I was most interested in the logarithmic amplifier circuits, which rely on the exponential relationship between current and voltage on a pn junction—often the emitter-base junction of a bipolar transistor.

My son wanted to know what the output range of the log amplifier would be and whether he would need another stage of amplification after the log amplifier. Unfortunately, the theory of the log amplifier uses the Shockley ideal diode equation, which needs the saturation current of the pn junction—not something that is reported for transistors.  There is also a “non-ideality” parameter, that can only be set empirically.  So we couldn’t compute what the output range would be for a log amplifier.

Today I decided to build a log amplifier and see if I could measure the output.  I also wanted to figure out what sort of dynamic range he could get from a log amp. Here is the circuit I ended up with, after some tweaking of parameters:

The top circuit is just a bias voltage generator to create a reference voltage from a single supply. I’m working off of 5v USB power, so I set the reference to 2.5v. He might want to use a 1.65v reference, if he is using 3.3v power.
The bottom circuit is the log amplifier itself.

I chose a PNP transistor so that Vout would be more positive as the input current got further from Vbias.  I have 6 different PNP transistors from the Iteadstudio assortment of 11 different transistors, and I chose the A1015 rather arbitrarily, because it had the lowest current gain. I should probably try each of the other PNP transistors in this circuit, to see how sensitive the circuit is to the transistor characteristics.  I suspect it is very sensitive to them.

The circuit only works if the collector-base junction is reverse-biased (the usual case for bipolar transistors), so that the collector current is determined by the base current. The emitter-base junction may be either forward or reverse biased.  Note that if Vin is larger than Vbias, the collector-base junction becomes forward-biased, the negative input of the op amp is slightly above Vbias, and the op amp output hits the bottom rail.

As long as Vin stays below Vbias, the current through R2 should be , and the output voltage should be for some constants A and B that depend on the transistor. Note that changing R2 just changes the offset of the output, not the scaling, so the range of the output is not adjustable without a subsequent amplifier.

The 1000pF capacitor across the transistor was not part of the designs I saw on the web, but I needed to add it to suppress high-frequency (around 3MHz) oscillations that occurred. The oscillations were strongest when the current through R2 was large, and the log output high.  I first tried adding a base-emitter capacitor, which eliminated the oscillations, but I still has some lower-frequency oscillations when the transistor was shutting off (very low currents).  Moving the capacitor to be across the whole transistor as shown in the schematic cleaned up both problems.

I put ramp and sine wave inputs into the log amplifier.  The waveforms were generated with the Bitscope function generator, which does not allow setting the offset very precisely—there is only an 8-bit DAC generating the waveform.  Here is a sample waveform:

Click picture for larger image. The green trace is the input, the yellow trace is the output. The horizontal axis in the middle is at 2.5V for the input (so the input is always below 2.5V) and at 3V for the output. The scale is 1V/division for the input and 50mV/division for the output.  [And all those values should be visible in the saved snapshot, but they aren't.]

Using the cursors on the BitScope, I was able to measure the output voltages for input voltages of Vbias-0.5V, Vbias-1V, and Vbias-2.5V.  From these, I concluded that the scaling factor for the output was about 3.1–3.2 mv/dB.  The output was 3±0.07V, so the dynamic range is 140mV/(3.2 mv/dB), or about 44dB.  We can see the logarithmic response in an X-Y plot of the output vs the input:

(Click for larger image) Output vs. input of the log amplifier. Note that the output is the log of Vbias-Vin, so the log curve looks backwards here.  It’s a shame that BitScope throws away the grid on XY plots, as the axes are still meaningful.

I also tried using an external oscillator, so that I could get better control of the offset voltage, and thus (perhaps) a better view of the dynamic range. I could fairly reliably get an output range of about 200mV, without the hysteresis that occurs when the collector-base junction gets forward biased. That would be over 60dB of dynamic range, which should be fine.

I should be able to adjust the voltage offset of the amplifier by changing R2. Increasing R2 reduces the current, which should lower the voltage. I tried several different values for R2 and measured the maximum output voltage, using the same input throughout:

The 60dB difference in current produces a 170mV difference in output, for 2.83 mV/dB.

Oops, those weren’t quite all the same, as the load from the resistor changes the input. Adding a unity-gain buffer driving the inputs and adjusting the input so that the output of the unity gain buffer has a slight flat spot at 0V gives me a new table:

which is consistent with 3mV/dB. I was not able to extend this to lower resistances, as I started seeing limitations on the output current of the op amp. But it is clear that the amplifier can handle a 75dB range of current, with pretty good log response.

An Arduino input is about 5mV/count, so the resolution feeding the output of the log amplifier directly into the Arduino would be about 1.7dB/count. We could use a gain of 4 without saturating an op amp (assuming that we use 2.5V as the center voltage still), for about a 0.4 dB resolution. More reasonably, we could use a gain of 3 to get a resolution of about 0.54dB/count.

I tried that, getting the following table:

This table is consistent with 9.1 mv/dB, for a resolution of about 0.54 dB/step on the Arduino.

I tried using the Arduino to collect the same data and fit with gnuplot:

(click plot to see larger version) The gnuplot fit agrees fairly well with the measurements made with the BitScope for 5 resistor values. The resolution of the Arduino DAC limits the ability to measure the dynamic range, and the cloud of points is broad enough to be consistent with slightly different parameter values.

The next thing for me to do on the log amp is probably to try different PNP transistors, to see how that changes the characteristics. My son will probably want to use a surface-mount transistor, so we’ll have to find one that is also available as a through-hole part, so that we can check the log amplifier calibration.

Yesterday, in Logarithmic amplifier, I ended with the following plot:

(click plot to see larger version) The cloud of points is broad enough to be consistent with slightly different parameter values.

I was bothered by the broad cloud of points, and wanted to come up with a better test circuit—one that would give me more confidence in the parameters.  It was also quite difficult to get close to Vbias—the closest this could measure was one least-significant-bit of the DAC away (about 5mV).  A factor of 512 from the largest to the smallest signal is 54dB, but only about the upper 40dB of that was good enough data for fitting (and very little time was spent at near the Vbias value).

I think that part of the problem with the cloud was that the input signal was changing fairly quickly, and the Arduino serializes its ADC, so that the input and output are measured about 120µsec apart.  I decided to use a very simple slow-changing signal: a capacitor charging toward Vbias through a large resistor.  My first attempt used a 1MΩ resistor and a 10µF capacitor, for a 10-second time constant:

Output voltage from log amplifier (with 3x gain in second stage) as capacitor charges. (click picture for larger version) One fit uses the Arduino-measured Vin and Vbias voltages, the other attempts to model the RC charging as well. What are the weird glitches?

The capacitor charging should be a smooth curve exponential decay to Vbias, so the log amplifier output should be a straight line with time. There were two obvious problems with this first data—the output was not a straight line and there were weird glitches about every 15–20 seconds.

The non-straight curve comes from the capacitor not charging to Vbias. Even when the capacitor was given lots of time to charge, it remained stubbornly below the desired voltage. In think that the problem is leakage current: resistance in parallel with the capacitor. The voltage was about 1% lower than expected, which would be equivalent to having a 100MΩ resistor in parallel with the capacitor.  I can well believe that I have sneak paths with that sort of resistance on the breadboard as well as in the capacitor.

According to Cornell Dublier, a capacitor manufacturer, a typical parallel resistance for a 10µF aluminum electrolytic capacitor would be about 10MΩ [http://www.cde.com/catalogs/AEappGUIDE.pdf‎]:

Typical values are on the order of 100/C MΩ with C in μF, e.g. a 100 μF capacitor would have an Rp of about 1 MΩ.

So I may be lucky that I got as close to Vbias as I did.

The glitches had a different explanation: they were not glitches in the log amplifier circuit, but in the 5V power supply being used as a reference for the ADC on the Arduino board—I had forgotten how bad the USB power is coming out of my laptop, though I had certainly observed the 5V supply dropping for a second about every 20 seconds on previous projects.  The drop in the reference for the ADC results in a bogus increase in the measured voltages.  That problem was easy to fix: I plugged in the power supply for the Arduino rather than running off the USB power, so I had a very steady voltage source using the Arduino’s on-board regulator.

(click picture for larger version) With a proper power supply, I get a clean charge and the output is initially a straight line, but I’m still not getting close to Vbias. Again the blue fit uses the measured Vin and Vbias voltages, while the green curve tries to fit an RC decay model. Note the digitization noise on the measured inputs towards the end of the charging time.

To solve the problem of the leakage currents, I tried going to a larger capacitor and smaller resistor to get a similar RC time constant. At that point I had not found and read the Cornell Dublier application note, though I suspected that the parallel resistance might scale inversely with the capacitor size, in which case I would be facing the same problem no matter how I chose the R-vs-C tradeoff. Only reducing the RC time constant would work for getting me closer to Vbias.

Using a 47kΩ resistor and a 470µF capacitor worked a bit better, but the time constant was so long that I got impatient:

(click image for larger version) The blue fit is again using the measured Vin and Vbias, and has a pretty good fit. The green fit using an RC charge model does not seem quite as good a fit.

The calibration of 9.7mV/dB seems pretty good, so the 409mV range of the recording corresponds to a 42dB range. The line is straighter, but I’m still not getting as close to Vbias as I’d like.

I then tried a smaller RC time constant (hoping that the larger current with the same capacitor would result in getting closer to Vbias, and so testing a larger dynamic range on the log amplifier). I tried 16kΩ with the 470µF capacitor:

(click image to embiggen) I’m now getting a clear signal from the log amplifier even after the input voltage has gotten less than one least-significant-bit away from Vbias (the blue fit). I found it difficult to fit parameters for modeling the RC charge (the green fit).

The two models I fit to the data give me somewhat different mV/dB scales, though both fit the data fairly well. The blue curve fits better up to about 65 seconds, then has quantization problems. Using that estimate of 9.8mV/dB and the 560mV range of the output, we have a dynamic range here of 57dB. There is still some flattening of the curve—we aren’t quite getting to the Vbias value, but it is pretty straight for the first 50 seconds.

Note: the parallel resistance of the capacitors would not explain the not-quite-exponential behavior we saw in the RC time constant lab, since those measurements were discharging the capacitor to zero. A parallel resistance would just change the time constant, not the final voltage.

I was using the Duemilanove board for the log-amplifier tests. I retried with the Uno board, to see if differences in the ADC linearity make a difference in the fit:

(click to embiggen) Using the Uno Arduino board I still had trouble with the fit, and the Uno ADC seems to be noisier than the Duemilanove ADC. The missing parts of the blue curve are where the Uno board read the input as having passed Vbias.

The 625 mV range over 250 seconds corresponds to about 69dB, assuming that the 9.1 mV/dB calibration is reasonably accurate (and 64dB if the earlier 9.8mV/dB calibration is better).
My measurements of the log amplifier do not seem to yield a very consistent mV/dB parameter, with values from 9.1mV/dB to 9.8mV/dB using just the Arduino measurements (and even less consistency when a model of RC charging is used).  I’m not sure how I can do more consistent measurements with the equipment I have.  Anyone have any ideas?
Incidentally, my son has decided not to include a microphone in his project.  The silicon MEMS mic was small enough, but the op amp chip for the analog processing was too big for the small board area he had left in his layout, and he decided that the loudness detector was not valuable enough for the board area and parts cost. I believe that his available board area shrunk a little today, because he discovered that the keep-away check had not been turned on in the Eagle design-rule checker.  Turning it on indicated that he had packed the capacitors too close in places, and he had to spread them out. (At least, I think that’s what he told me—I’ve not been following his PC board layout very closely.)
I’m still interested in learning about log amplifiers and precision rectifiers, so I’m still going to breadboard the components of the design and test them out.  I’m not sure when I’ll ever use the knowledge, since the Applied Circuits course does not cover the nonlinear behavior of pn junctions nor the forward-voltage drop of diodes (we don’t use diodes in the course).

The log amplifier that I’ve spent the last several days understanding (posts a, b, c) is not the only non-linear circuit needed for a loudness detector.  We also need to convert the audio input signal into a slowly changing amplitude signal that we can take the logarithm of.  As I discussed in the first post on log amps, I had rejected true-RMS converter chips as too expensive for the application (though the original application has gone away), and decided to try a rectifier and low-pass filter.

[Incidentally, my son is now looking at a different processor chip, the KL25 from Freescale (an ARM Cortex chip), which has a 16-bit ADC that is much faster than the ATMega's, so the entire loudness-detector could be done in software, except for a one-op-amp preamplifier.  With a  16-bit ADC, we can get almost 90dB of range without needing a log amplifier. We're planning to order a development board that is compatible with Arduino shields (but has lots more I/O pins available) and that has an accelerometer on the board.  Amazingly, the development board is only $13, about half the price of an Arduino.]

A single diode does not work for our rectifier needs in the loudness circuit, because diodes don’t turn on until the voltage across them is at least a “diode drop” (about 0.7v for silicon diodes and 0.45v for Schottky diodes).  However, the simple circuit for the log amplifier is also the circuit for a precision rectifier:

This circuit is both a log amplifier and a precision rectifier. If Vb is set to a constant voltage, then Vout1 varies as log(Vb–Va). Vout2 is max(Va,Vb). 
The diode can be connected in the opposite direction, to get Vout2=min(Va,Vb) and Vout1 varying with log(Va–Vb).

The log-amplifier circuit I used in the previous posts had a transistor in place of the diode, so that the crucial voltage that was being exponentiated was referenced to the bias voltage, rather than the input. We also needed a compensation capacitor in parallel with the transistor to prevent oscillation in the negative feedback loop.

For the precision rectifier, we swap the inputs, so that Va is the signal input and Vb is a constant threshold voltage for the rectifier. We do not need (or want) the compensation capacitor, as that would cause the circuit to act as a unity gain amplifier at high frequency, rather than as a rectifier.

Because I did not happen to have any diodes, but had plenty of transistors, I experimented with the rectifier circuit using diode-connected bipolar transistors (collector and base connected together). Because the output of the rectifier is not directly driven by an op amp, I used unity-gain buffers to isolate the test circuitry (Arduino analog inputs or BitScope oscilloscope) from the amplifier:

Test circuit for low-speed testing of precision rectifier circuit. Here the NPN transistor is used as a diode, in the opposite direction as in the first schematic, so Vout should be min(Vin, Vbias)

My initial test setup did not have the unity-gain buffer for Vin, but I found that one of my Arduino analog input pins was quite low impedance and was discharging my capacitor. Switching to a different pin helped, but I eventually decided to avoid that kluge and use a unity-gain buffer instead.

I tried several different values for R₂. The most predictable effect of changing the value is a change in the range over which the rectifier operates. Clipping occurs because the output of the op amp is limited to be between the rails of the power supply. The feedback transistor is conducting when the rectifier is following the input, so the op amp output has to be substantially lower than Vout.  The function implemented is max(Vclip, min(Va,Vbias)).  Vclip should go down as R₂ is increased (at about 60mV for each factor of 10 in resistance—the same shift as in the log amplifier).

Here are a couple of plots of Vout vs. Vin for the S9018 transistor:

(click to embiggen) With a 1kΩ resistor, the clipping voltage is fairly high, and we have a somewhat limited range for the rectifier.  The offset voltage for the rectifier between the output and the input is much less than the resolution of the Arduino ADC (about 5mV).

(click to embiggen) With a 10kΩ resistor, the clipping voltage is lower, giving us more range for the rectifier.

Using a PNP transistor instead of an NPN has the effect of reversing the diode and producing Vout=min(Vclip, max(Vin, Vbias)):

(click to embiggen) With an S9012 PNP transistor and a 1kΩ resistor, we get clipping at the high end.

(click to embiggen) With a 10kΩ resistor we get a larger range.

So why not go for a very large resistor and maximize the range? From a DC perspective this looks like a win (though it is hard to see in the limit how Vbias would affect the result if the resistance went to infinity).  Of course, the problem is with high-frequency response.  Consider the difference between the S9018 NPN transistor with a 1kΩ resistor and a 330kΩ resistor:

(click to embiggen) With an S9018 NPN transistor and a 330kΩ resistor at 1kHz. Note the overshoot when the rectifier shuts off.

(click to embiggen) Fairly clean signal with a S9018 NPN transistor and a 10kΩ resistor at 1kHz.

(click to embiggen) With a 1kΩ resistor, there is very little overshoot as the rectifier turns off, but we can see a bit of a problem when the rectifier turns back on.

There is a problem with the rectifier turning on slowly, because Vout has to move all the way from the top rail down to the bias voltage, and the op amp has a slew-rate limitation. This phenomenon can be seen more clearly at a higher frequency:

(click to embiggen) The S9018 NPN transistor with a 10kΩ resistor and a 15kHz input signal. The overshoot as the rectifier turns off is about 50mV, and the turn-on delay is about 8µsec. The turn-on delay does not vary much with the input resistance, unlike the turn-off overshoot.

I believe that the overshoot as the rectifier turns off is due to capacitance, as adding a small feedback capacitor in parallel with the diode increases the overshoot substantially:

(click to embiggen) With a 33pF capacitor in parallel with the diode (an S9018 NPN transistor), a 10kΩ resistor, and a 15kHz input, the overshoot goes up to about 290mV from 50mV without the capacitor. The turn-on delay is masked somewhat by the high-frequency feedback.

Note: the S9018 has the best high-frequency response (if you consider 15kHZ high frequency) of any of the transistors I looked, probably because it has the lowest capacitance. For example, with a 10kΩ resistor the S9013 NPN has 120mV of overshoot at 15kHz, instead of only 50mV, and the S9012 PNP has -180mV. With a 1kΩ resistor, I can’t measure the overshoot on any of these three transistors. So the limited range with a 1kΩ resistor is compensated for by the much cleaner turn-off behavior.  I should be able to get better range by using a fast-response Schottky diode instead of diode-connected transistor.

Of course, the turn-on behavior is a bigger problem and one that can’t be fixed by playing with the resistor or the diode, because the problem is with the large voltage swing needed from the op amp in order to turn on. There are standard solutions that limit the voltage swing, but I think I’ll leave that for a later blog post.

In the Precision rectifier post, I gave the simplest circuit for making a precision rectifier:

This circuit is both a log amplifier and a precision rectifier. If Vb is set to a constant voltage, then Vout1 varies as log(Vb–Va). Vout2 is max(Va,Vb). 
The diode can be connected in the opposite direction, to get Vout2=min(Va,Vb) and Vout1 varying with log(Va–Vb).

And I showed the problem with this circuit at “high” frequency, as the slew rate limitations of the op amp limit the turn-on time (to about 8 µs):

(click to embiggen) The S9018 NPN transistor with a 10kΩ resistor and a 15kHz input signal. The overshoot as the rectifier turns off is about 50mV, and the turn-on delay is about 8µsec. The turn-on delay does not vary much with the input resistance, unlike the turn-off overshoot.

I also promised, “There are standard solutions that limit the voltage swing, but I think I’ll leave that for a later blog post.”  This is that post.

The textbook standard solution is to add another diode and resistor, and to configure the rectifier as an inverting amplifier (rather than a unity-gain one) when it is following the input:

Only one of D1 and D2 can be conducting.

This circuit has an input impedance of R1 (not the very high input impedance of the previous circuit). In this circuit, if Vin is more than Vthreshold, the output of the op amp goes low until diode D1 conducts and the negative input of the op amp is held at Vthreshold, as is Vout (with an output impdeance of R2).  If Vin is less than Vthreshold, the output of the op amp rises until D2 conducts, and the feedback circuit makes an inverting amplifier with .  The output impedance is very low.  Note that the difference in the output impedance for the two states is similar to the situation for the simpler circuit, and can cause problems if the output of the rectifier is fed directly to an RC filter, unless the R value for the RC filter is much larger than R2.  For the loudness circuit, we want a very large RC time constant to smooth out the ripples of the rectifier, so a large R value is not a problem.

We expect this circuit to have problems when neither D1 nor D2 is conducting—that is, as the circuit makes transitions between the rectifier being on or off.  The simple rectifier circuit only had problems with turning on (as the op amp had to slew from a rail to a diode-drop past Vthreshold), but this improved circuit has to swing two diode drops when turning on or when turning off.  The two-diode-drop swing is smaller than the

Here is an example of the output with a 30kHz clock, using S9018 transistors as diodes and R1 and R2 both at 10kΩ:

(click to embiggen) Output (yellow) for the improved rectifier with a 30kHz triangle wave as input (green). The glitches are about 140mV–160mV and last for about 4 µsec.

The duration of the glitches is always about 4µs, but the magnitude of the glitches depend very much on frequency.  With a 2kHz triangle wave signal, I can’t see the glitches with the BitScope USB oscilloscope (so less than about 20mV).  The magnitude of the glitch seems to be proportional to the input magnitude. Using a constant amplitude triangle wave input (about 2.6v peak-to-peak),  I measured the glitches for some higher frequencies:

To understand where the glitches come from, it helps to look at the op-amp output and the negative feedback input:

(click to embiggen) The output of the op amp (green) is either a diode drop above or a diode drop below the output of the rectifier circuit (yellow) depending which diode is conducting.  The transitions between these states are limited by the op amp slew rate.  I measured about 600 mV/µsec, which is what the MCP6002 op amp I’m using is specified to have as a slew rate (I measured before looking it up, to keep from being biased by the “correct” answer).

(clcik to embiggen) The negative input of the op amp (green), which the feedback circuit is trying to keep at Vthreshold, has glitches when the op amp output (yellow) is ramping between its two states.

The glitches in the improved circuit are smaller than for the simpler circuit, and can be further reduced by using Schottky diodes (to reduce the size of the diode drop, and hence how far the op amp must swing to change states) or a faster op amp (to reduce how long the op amp takes to slew the two diode drops).  I expect that with the Schottky diodes, the glitches should be reduced to 2(450mV)/(600 mV/µs)=1.5µs.  Since the glitches are basically triangular pulses, reducing the duration by a factor of 2–3 should reduce the amplitude by as much, and the total energy by 8–27.

To test the rectifier circuit with better diodes, I’ve ordered some 1N5817 Schottky diodes from Digi-key. I like dealing with that company, as they have a lot of components I need, are always very fast in processing orders, and have not yet messed up an order.  They were once out of stock on something that I had ordered, and called me up to apologize profusely for the mistake in their inventory database (normally they notify you before you order if something is out of stock).  For today’s order, they sent me notice that they had shipped the order less than an hour and a half after I had placed the order.  Because they offer first-class US mail as a shipping option, their shipping charges tend to be much less than most of the places I deal with.  (UPS ground is cheaper for big things, but no one is beating the Post Office prices on small lightweight objects.)

Disclaimer: neither Digi-key nor the Post Office has offered me anything for my endorsement—I’m just feeling pleased with them right now.

In the Improved rectifier post, I gave the following circuit for an inverting rectifier and showed traces of its performance using diode-connected S9018 NPN transistors as diodes:

Only one of D1 and D2 can be conducting.

With a constant amplitude triangle wave input (about 2.6v peak-to-peak),  the circuit had some pretty serious glitches:

I claimed that I could reduce the glitches  by replacing the NPN transistors with 1N5817 Schottky diodes.  The diodes arrived today, and I tried them out with the same 10kΩ resistors and 30kHz triangle wave as before:

(click to embiggen) With the 1N5817 Schottky diodes, the glitches at 30kHz are much reduced—only about 68mV of overshoot when turning off, which is half of the glitch with the S9018 NPN transistors as diodes.

I noticed that there was a bit of phase shift for the 30kHz signal, as well as the small overshoot. I tried adding capacitors in parallel with the resistors to improve the performance at 30 kHz (both to correct the phase shift and to keep the gain at -1).

This circuit works well up to 30kHz, and is still somewhat functional at 100kHz

C2 seems to adjust the overshoot, and C1 then needs to be set to fix the phase and gain.  I had the best results at 30kHz with C1=330pF and C2=220pF:

(click to embiggen) With capacitors in parallel with the feedback resistors, the phase shift is mostly corrected and there is less than 20mV of overshoot—the turn-on and turn-off corners are softened somewhat.

Unfortunately, there is no easy way in the BitScope software to set the offset of the traces precisely. You can do a lot of range changing and clicking the left or right sides of buttons (and start all over if you accidentally hit the middle of the button), but the offset is only displayed to 2 decimal points, but can be adjusted somewhat finer, making it hard to guess exactly what it is set to. As result, I’ve not been able to measure the overshoot or undershoot when it is less than 10mV—I’m never sure exactly what I’m measuring with respect to, and visually similar settings result in ±10mV in the estimate. In any event, the errors in this version of the improved rectifier are at least 5× better than in the version with the S9018 diode-connected transistors.

The circuit works well throughout the audio range, and can be pushed to 100kHz, though the “corners” have gotten soft enough that clipping to the threshold voltage is no longer very precise at (about 60mV off @ 80kHz—undershoot, not overshoot). At 100kHz, the output signal is still pretty good, but there is about an 85mV error in the threshold, and the corners are so rounded that the output almost looks like a sine wave:

(click to embiggen) Waveform at 100kHZ (sine wave input), showing the soft corners at that frequency. The output does not get down to the threshold voltage, but only to about 85mV above threshold.

I can get better performance at 100kHz with smaller capacitors (100pF and 220pF, instead of 220pF and 330pF), but at the cost of some overshoot at 20kHz and 30kHz.  I suspect that the right values for the capacitors depend heavily on what op amp is used (especially its slew rate), but since I only have MCP6002 (and the equivalent MCP6004) op amps, I’ve not tested this suspicion.

One hears about bloggers making money off their blogs from advertising (I get nothing from the ads that WordPress.com puts on my blog—it just pays for the free blogging service).  One also hears about bloggers getting sent products or books to review on their sites, as a form of cheap advertising.  I’ve reviewed a number of things on my blog, but they’ve always been things I’ve bought retail, not promotional items.

Yesterday I got my first free swag.  Bitscope liked my use of their Pocket Analyzer USB oscilloscope in my circuits blog posts, and are supposedly integrating some of my suggestions into their next software release.  They offered me a chance to use and review a pre-production version of a new product: a front-end for the Pocket Analyzer that gives it the ability to do true differential inputs and AC coupling, reducing some of the limitations of the DC-coupling and having the analog ground be the same as the USB ground.

I agreed to this on 2013 July 29, and they supposedly sent me one of the devices.  I never got it, though, thanks to the combination of the Australian and US post offices (perhaps it is still on a boat circling the Pacific Ocean). Had I gotten the device over the summer, I would have probably spent a week playing with it, reporting the results on my blog. Now that the Fall quarter is in full swing, I’ll have much less time, what with teaching classes, grading programs, supervising grad students, and helping write grant proposals. I’ll probably be only able to put in an hour or two a week on it (I’ve already spent far more than that today on this blog post, and I’ve still not done any meaningful testing).

Bitscope asked me last week when I was going to post something, and I told them that I was still waiting to get something.  So they sent me another one via Fed Ex, which came quite promptly:

I found the routing a little strange (Los Angeles->Memphis->Oakland), but I can’t fault the delivery speed. Within the US, I’ve always had very good service from the US Post Office, with prompt, low-cost delivery, but deliveries across the Pacific can be a bit iffy. It generally takes 2–3 weeks to get something from China through the Post Office, longer from India, and my success rate from Australia is only 50% (small sample, though). It may be worth paying extra for more reliable shipping from Australia and India.

The probe PC board is about 6.2cm long and 2cm wide (8cm long with the connectors on the ends).

The back of the probe has a connector with 3 twisted pairs that go to the Pocket Analyzer, and two jumper positions for shorting plugs that change the gain of the preamplifiers in the differential probes. The label on the probe says 2× without the jumper and 20× with the jumper, but I was told by email 0.5× and 5×, so I’ll need to test the gain for myself. There is no documentation yet, since this is a pre-production prototype.  The jumpers for gain switches are a bit of a kluge, but I expect that sort of cost cutting on a USB oscilloscope.

The other end of the short (~14cm) cable from the probe plugs into the leftmost pins of the Pocket Analyzer, connecting to 5v, 3.3v, A, B, and 2 Gnd pins. There are two blank positions on the left end of the connector, corresponding to the space at the end of the connector on the Pocket Analyzer. I suspect that the intent is to use this as a key to reduce the probability of plugging the probe in wrong. It probably won’t help much, as there is nothing stopping anyone from plugging it in upside down at the wrong end of the connector—the Pocket Analyzer uses a symmetric connector that has no keying.

On the component side, we can see that there are are 4 main ICs (probably op amps or instrumentation amps, but I can’t read the labels through the heat-shrink tubing) and a number of discrete components. I’m assuming that the heat shrink tubing is a pre-production measure, and that they’ll have a classier-looking case once they go into production. (I’ve been recommending heat-shrink wrapping for the LEDs in the light gloves my son in designing, because I think that classier cases for the LEDs will be difficult for them to get made in tiny quantities, but I suspect that BitScope is looking at a larger production run than the first run for the light gloves).

Taking a closeup photo of the input end of the probe with my camera lets me see the labels on the ICs. They seem to be MCP6292 E/SN chips (about 67¢ each from DigiKey in 100s).  Those are dual rail-to-rail op amps with a 10MHz gain-bandwidth product (7v/µs slew rate), with a 2.4v–6v single-sided power supply.
You can also see that the surface mount components have been hand-soldered, by someone who is worse at SMD soldering than me (that’s pretty bad). It looks to me like one of the components (a resistor?) has been shorted by a bad solder bridge. I assume they did some testing before sending me the probe, so I hope that this is an optical illusion, not a real short.

I’ve not heard back from the BitScope folks yet what voltage range is acceptable on the inputs, so I’ll have to be rather cautious at first—the op amps don’t want inputs more than 1v outside the op-amp power rails, and I don’t know what voltage dividers there are before the op amp.

I suspect that the bandwidth for the probe is around 5MHz in the low-gain setting, and 1MHz in the high-gain setting—I’ll probably have to take the setup into one of the student labs at the university to test this, though, as I don’t have much to use for comparison at home. It may be difficult to measure the bandwidth when the probe is plugged into the Pocket Analyzer, since the Pocket Analyzer itself has limited bandwidth. I can’t get it to sample faster than 5MHz, which gives an upper limit of 2.5MHz for the bandwidth. The online documentation for the BitScope claims 20M samples/sec is possible, but if I try to set that, the software claims that there is an access violation and does not change the setting.

I think that the noise floor of the differential probe will also be set by the rather high noise in the Pocket Analyzer. The high-gain setting of the differential probe will allow somewhat better signal-to-noise ratios, as I doubt that the differential probe is anywhere near as noisy as the Pocket Analyzer, which seems to have ±3LSB on an 8-bit DAC (about ±1% of full scale). I wonder whether BitScope will try to take advantage of some of the newer processors (like the Freescale Kinetis L family) that have higher resolution ADC with probably adequate sampling rates.

In First blogging swag, I mentioned getting a pre-production prototype of the Bitscope DP01 Dual Channel Active Differential Probe:

The probe PC board is about 6.2cm long and 2cm wide—8cm long with the connectors on the ends. (More pictures in First blogging swag)

Because the first one they sent me got lost in the mail, I didn’t get this device until the Fall quarter had started and I had a lot of grading to do every weekend (plus trying to rewrite the bioengineering and bioinformatics curricula, but that’s a subject for a different blog post).  This weekend I finally have a long weekend without grading (I’ll pay for that next weekend, with a double or triple load), so I’m going to indulge myself and play with my new toy.

The BitScope folks have not released a full spec sheet for the device yet, but they have a blog post with the essentials (and now the official DP01 web page):

DP01 | Active Differential Probe Specifications

The bandwidth for the probe is probably larger than the bandwidth for the BS10U Pocket Analyzer itself, and low-voltage measurements will be limited by the noise floor of the pocket analyzer. Let’s start by looking at the pocket analyzer with shorted inputs, to see what the noise floor is:

Here is the waveform for the shorted inputs at the highest gain the BitScope provides (10mV/division) at a fairly high sampling rate (5µs/division). The peak-to-peak noise is about 14mV, and the digitization noise (about 2mV/step) is clearly visible. (Click to embiggen.)

For those who have taken my classes and know how I rail against the insanity of black backgrounds and unlabeled axes for plots, I apologize, but BitScope still provides only this 1950s style display, even with the development version of the software (DSO 2.7 DG17G). I wish they would produce publication-quality displays (in svg or pdf formats, with no black background), but I suspect that they have only electrical engineers on their development team, with no graphic designers or human-computer interface experts. It would do them a world of good to read Tufte’s books or some other basic introduction to displaying information.

Click to embiggen. Here is the “spectrum” display of the waveform in the previous image (BS10U Pocket Analyzer with shorted inputs). The vertical scale is 10dB/division, and the horizontal scale is 0.6MHz per division (what an awkward unit!). It would be really nice if there were an option to get a log scale on frequency, as is done on Bode plots.
The big spike marked with the vertical orange line is at 2.5 MHz, and is pretty consistently present.  The horizonal orange line is at 25dB, and the vertical axis is 10dB/division.

The noise seems to be low-pass filtered at about 2 or 2.5MHz (it’s a little hard to tell, since there is no way with the Bitscope sample to take a really long sample and smooth out the random fluctuations), dropping about 120dB per decade above the cutoff. That would be 6th-order filter, which seems a little high order for an anti-aliasing filter. More likely, they are using a lower-order elliptic filter, Chebyshev filter, or other design with a sharp transition between the passband and the stopband. That might also explain the peaking at 2.5MHz, though the peak seems too sharp to be a filter artifact. Using just the amplifier input noise to probe the filter does not give me much information about the filter once it starts attenuating, so I don’t know what the stop band looks like.

Unfortunately, “The spectrum magnitude display is unreferenced; all measurements are relative to the prevailing V/Div value on each channel” (http://www.bitscope.com/software/dso/guide/2.5/?p=spectrum), so I don’t know what 25dB means here in terms of the actual noise density. A 350mV peak-to-peak sine wave is 60dB  at 100mV/division, and 80dB at 10mV/division, so 25dB at 10mV/division would be about 600µV peak-to-peak or 220µV rms for a sine wave.  I’m too lazy to try to figure out the rms V/√Hz noise density.

Adding the differential probe in front of the Pocket Analyzer does not change the spectrum shape noticeably.

Waveform (using sharp, raw data display) at 5µs/division and 2mV/division of shorted inputs to the DP01 differential probe at high gain (supposedly a gain of 5). (click to embiggen)

The spectrum (using the sharp, raw data display) looks essentially the same as without the DP01 probe. Note how sharp the 2.5MHz peak is in this view. The limitations of the Pocket Analyzer mask any limitations of the DP01 probe. (click to embiggen)

In the high-gain mode, the probe has a gain of 5 and the input-referenced noise is around 6mV peak-to-peak, instead of 14mV peak-to-peak without the probe. In the low-gain mode (gain of 0.5), the input-referenced noise is about 26mV peak-to-peak (4 different quantization levels). There is noise added by the probe in the high-gain mode, but it is still better than the Pocket Analyzer without the probe (about 7dB better signal-to-noise ratio, though a gain of 5 should produce a 14dB gain.

I looked at the output of my Elenco Model FG-500 function generator with about a 292kHz waveform (80mV peak-to-peak with about a 4.1v DC offset): one channel set to high gain with AC coupling, the other set to low gain with DC coupling and mean-subtraction in software.

With high gain and AC coupling (yellow), the 292kHz ~80mV signal is easily seen, but with DC coupling (green) the gain has to be turned down to get enough range, and then the low resolution of the BitScope’s ADC is a problem. (click to embiggen)

The glitches in the “sine wave” output of the FG-500 function generator are actually much bigger than they appear here. With my 60MHz Kikusui COS 5060 analog oscilloscope, I can see a downward spike from the top of the sine wave of about the same magnitude as the sine wave in about 30nsec—much faster than the BitScope Pocket Analyzer can capture.

Spectrum at 20 mv/division shows the harmonic distortion and a clear 20dB larger noise floor for the low-gain signal than the high-gain, AC-coupled signal. (click to embiggen)

So far, I’ve just been looking at the probe as an amplifier, without taking advantage of the differential inputs.

I did a simple test with the Freedom KL25Z board (which has a 12-bit DAC), outputting 17 values (0, 0×200, 0×400, … 0×2000), where the full range of the DAC  is 0, 0×10, …, 0xfff0.  I used a series resistor and capacitor as a load, and measured the voltage across each.  Since both the Freedom board and the BitScope are being powered from the same USB supply (my laptop), having  differential inputs really reduces the risk of possibly shorting a signal to ground, and allows me to measure the voltage across the capacitor and the current into it simultaneously.

I connected a 470pF capacitor and a 1802Ω resistor in series as a load for the KL25Z 12-bit DAC, and measured the voltage across each. Channel 1 in yellow is the voltage across the resistor.
Channel 2 in green is across the capacitor. As expected the current through the resistor is the derivative of the voltage across the capacitor, but why the small spikes as well? (click to embiggen)

(click to embiggen) With the capacitor removed, the current drops to 0, and the voltage shows bad behavior for the DAC when it switches from 0xe00 to 0×1000 and from 0x1e00 to 0×2000.
I checked, and there are similar problems at all the multiples of 0×1000, even coming from just one count lower.

The KL25 specs call for a settling time of <1µs for single steps and <30µs rail-to-rail. I’m seeing a faster slew than that for large changes (about –3V/1µs slew rate), but the glitch at the multiples of 0×1000 is almost a microsecond long, so is pushing against the code-to-code spec.

Incidentally, it looks like I can output values to the KL25 DAC at about 828kHz with the mbed libraries (using write_u16(), not their ridiculously slow floating-point output routine).  Given the 1µs settling time, there isn’t much point to trying to push it faster than that.

Overall, the DP01 seems like a useful tool, compensating for many of the weaknesses of the BitScope Pocket Analyzer. The AC coupling, the differential inputs, and the increased gain are all useful features.  There are some flaws, though:

• Changing between differential and AC-coupled input by changing the orientation of the connectors is annoying, and it is very easy to connect things up wrong.
• Having to use shorting plugs to change the gain is also annoying—especially since the labels on the pre-preduction release I have suggest a different arrangement of the shorting plugs than the one that actually works. See the picture at the beginning of this post—the plugs have to be horizontal, with channel 2 on top, but the label suggests that they are vertical, with channel 1 on the outside.  Of course, the label also suggests that the gain is ×2 and ×20, rather than ×0.5 and ×5—I hope that they fix that confusion in the final release.
• Having to remember to change the gain setting on the software every time the gain is changed is also annoying.  A more integrated  system would communicate the gain settings of the probes to the software automatically (difficult to do through the Pocket Analyzer, though, since it has no communication with the probe other than power and measuring the analog output).

Overall, I’m moderately pleased with the BitScope hardware, but I still find their software poorly designed and poorly implemented.  Plots have unlabeled axes, cursors can’t be nudged with arrow keys, and numbers can’t be typed in—everything has to be done by microscopic movements of a mouse, which is doubly difficult on a laptop trackpad.  I had several array-out-of-bounds crashes today, and the few cryptic labels that are on the plots are often wrong (changing the time base does not update the frequency computation for “FP”, for example).

I’m considering using the DP01 preamplifier before the analog-to-digital converters on the Freedom KL25Z board. I may not get all the flexibility of the BitScope that way, but the 16-bit ADC may compensate for a lot of problems. I should be able to get down to a resolution of 10µv that way, which may be enough to do an EKG recording without an additional amplifier.  Unfortunately, I won’t be able to view traces easily, as I’ve not yet gotten my son to rewrite the Arduino Data Logger to talk with the KL25Z board—he’s been spending all his programming time on his light gloves project, and when I can get his attention, it is usually to insist that he work on his college application essays.

I was thinking about things we might do in the first lab day for the Applied Circuits course next quarter, now that I have 2 lab sessions a week.  The first, obvious thing is to unpack the lab kits and identify the different components, labeling the capacitor zip locks with values of the contained capacitors, and learning to use the wire strippers, the power supplies, and the voltmeters.

I’m thinking that I should have the students make a 3′ red-black twisted pair and pack it with their parts, so that they don’t try getting new power wires every week.

One experiment I was considering having them do is to look at the AC signal from a large loop of wire and from twisted pair, to see the difference in noise pickup.  I tried doing this at home today, with rather disappointing results.  The large loop did not pick up more 60Hz noise than the twisted pair when viewed on either my Kikusui oscilloscope or by Bitscope USB oscilloscope.  In fact I couldn’t see any noise with either one.

I tried adding my 1500-gain EKG amplifier as a front end, and then I could see about 60μV noise, but that did not change whether I used a long loop, a twisted pair, or a very short loop between the instrumentation amp inputs.

I first tried looking at how much noise there was from the Bitscope with the DP01 active probe using AC coupling:

Looking at shorted inputs for the AC-coupled DP01 active probe in its high gain mode. This is 2mV/division, 100µs/division, “macro” mode. The noise is a couple of mV, about the same as the noise level without the DP01, but the resolution is much better with the DP01.  The high-speed trace here is to show the component of the noise that is around 30.8kHz, which is about as big as the 60Hz component.  The 30.8kHz noise is most likely from the USB power supply into the Bitscope.  The Bitscope does not appear to have as good power-supply noise rejection as one might want.

I then hooked up the EKG amplifier board (which should have a gain around 1508) using a separate power supply, and looked at the noise on the Vref signal (which is just buffered from a voltage divider on the power supply).

At 2mV per division and 10ms per division, we can see a little 60Hz noise added to the high-frequency noise of the Bitscope, but the noise is still only 2–3mV, which would be an input-referenced noise of about 2µV given the amplifier gain around 1500.

The noise on Vref is not much more than noise inherent to the Bitscope and is very similar to the noise I see looking just at the output of the power supply without the EKG attached.
Next I looked at the output of the EKG, with both inputs shorted to Vref.

This is now 40mv/division and 10ms/division looking at the output of the EKG amplifer with both inputs shorted to Vref. The output noise is around 90mV, so the input-referenced noise is around 60µV.

Now we see a signal that is not just Bitscope or power supply noise, and have a noise floor for looking at signals at the input of the EKG amplifier.

Unfortunately, replacing the short with a large loop of wire does not appreciably change the signal, but if I connect the two EKG inputs to Vref via separate 2.2MΩ resistors, I get a large output:

200mV/division, 10msec/division. Inputs of EKG amplifier separately connected to Vref via 2.2MΩ resistors. This signal is about 1.04V peak-to-peak (so the input is about 690µV).

The output can be changed substantially by putting my hand near the resistors—the 60Hz noise appears to be capacitively coupled into the amplifier. I can reduce the peak-to-peak voltage to about 500mV  (that is around 300µV at the input) and make it have a larger 120Hz that is almost 10dB larger than the 60Hz component, , just by moving my finger around near the resistors. I can also raise the signal until the EKG amplifier is swinging rail-to-rail (at least 3mV at the input).

So I don’t have a demonstration circuit for electromagnetic pickup here, but I do have one for capacitive coupling.  To detect currents induced in a loop, I probably need a transimpedance amplifier to detect small currents, rather than an instrumentation amplifier to detect small voltages .  I’ll leave that for a separate post.

Today’s class started with feedback on their second design reports (the electret mic lab). Everyone in the class got a “redo” on this assignment.  Some of them actually had pretty good write-ups, but I had warned them that errors on schematics or with units would trigger automatic redos, and every report had at least one serious error (like 200A, instead of 200µA, or short-circuiting the mic). I’m going to hold them to getting their schematics and units right—details matter in engineering, and they have got to develop a habit of double-checking what they write.

After a little more feedback (on how to improve their plots, for example, and little details like capitalizing “Figure 1″ or using the prepositions with voltage and current), I switched to new material on hysteresis that they’ll need for tomorrow’s lab.  I actually gave them a fairly detailed description of hysteresis in the lab handout (I wonder if anyone has read it yet?), but I covered it again anyway. I also talked about DIP vs. SMD parts (the 74HC14N chip they’ll use is in a DIP), and introduced them to a simple relaxation oscillator.  We worked through how it functioned to produce a triangle wave on the input and square wave on the output, but I did not mention the capacitive coupling from the output to the input that changes the triangle wave rather dramatically when the capacitor in the RC circuit is small.

Input (yellow) and output (green) of a Schmitt-trigger relaxation oscillator (approx 67kHz). Note that the large output step is capacitively coupled to the input, causing a small step in addition to the expected triangle wave.  Note, the two traces are separate sweeps and the frequency modulation by 60Hz noise is big enough that the periods are not exactly the same on the two sweeps.  (click to embiggen)

The funny step in the input is not visible if large capacitors are used, but accounts for a big part of the charge transfer for small capacitors (throwing off the RC calculations that determine period).

With a 680kΩ resistor and a 10pF capacitor, attaching a BitScope probe to the input changes the period from about 4.5µs to about 14µs. With the same resistor and a 30pF capacitor, attaching the probe changes the period from 17.5µs to 28.5µs—the change due to the input impedance of the scope makes a big difference in the behavior of the circuit. I’ll have to make sure that the students observe the effect that a scope probe has on their circuit—they’re probably still thinking of the measurements as being non-disruptive.  (They may get even bigger changes in period with standard oscilloscope probes—with the 30pF capacitor I get periods of 220µs for a 1× probe and 30µs with a 10× probe on my Kikusui oscilloscope—the BitScope input is similar to the 10× probe.)

Last year’s hysteresis oscillator lab ran quite long, but I’m hoping for better time tomorrow. I went through the behavior of the oscillator a bit more thoroughly, and I think I impressed on them the importance of doing the algebra and calculations before lab time. I also suggested how they could find the input threshold voltages using PteroDAQ at home (triggering on both rising and falling edges).

Today’s lab went well, with very little intervention on my part. Students finished up their RC calculations, picked their resistors and capacitors, and got their relaxation oscillators working.  They then adjusted their R or C values to bring the oscillator into spec, if needed. Most of the help I gave during all this was getting the students comfortable with using the Tektronix digital scopes, which have an extremely complicated and confusing menu system. The “autoset” feature on the scopes is almost essential, since they can have been left in any sort of weird state by the previous user, and finding and clearing all the weirdness takes a while.

Students then made their touch sensors (aluminum foil folded up to be sturdy, then wrapped with a layer of packing tape), and connected them to the oscillators. Most students got a substantial change in frequency, as expected, but one group had chosen a large C and small R, and so got almost no change. With only minimal prompting, they figured out why the frequency wasn’t changing, fixed their values and got it working.

The students did observe a change in frequency if they connected a scope probe to the input of the Schmitt trigger, and most eventually figured out that this meant that the scope probe was acting like a capacitor.  When I did it with my scope probe at home, I got a change from 60kHz to 35.22kHz, about a 70% increase in the RC time constant.  Since the capacitor I was using was 30pF, this looks like it implies a 21pF capacitance.   It doesn’t make much difference whether I connect the scope ground to the ground or the 3.3v lead—the change in frequency is the same either way, so we’re seeing an effect due to capacitance, not due to current through the oscilloscope input resistance. I looked up the specs for the input capacitance of my probes, and it is supposed to be 20pF in 10× mode and 130pF in 1× mode.  From that I worked out an approximate circuit for the probe:

Approximate circuit for my cheap 60MHz scope probes.

With the 1× probe setting, the 1MΩ input resistance of the oscilloscope matters—connecting up the scope drops the oscillation frequency to 5kHz if the ground of the scope is grounded, and stops oscillation completely if the ground of the scope is connected to 3.3v.

The Bitscope DP01 differential probe, with no jumper plugs in place (so 2:1 setting on the Bitscope screen) reduces the frequency from 59.7kHz to 38.6kHz, implying about a 16.5pF input capacitance, while the spec claims only 2.5pF differential and 5pF common-mode. I don’t seem to be able to get a signal on the BitScope screen with the differential probe in high-gain mode, and I’m not sure why (the voltages shouldn’t be exceeding the voltage limits).  There may be some problem with powering both the BitScope and the device being tested from the same underlying USB power source, though it caused no problems in the low-gain mode.

Students soldered up the boards without problems. The only intermittent error that I had to help debug turned out to be a misuse of an alligator clip (the wire had not been screwed down, but only wrapped around the clip). No one soldered a chip in backwards and I did not need any of the spare boards or chips that I had brought along, just in case.

Luckily not everyone was ready to solder at the same time, as the lab support people had no board holders available, so only the two I brought from home were available.  I’ll have to ask them to get some PanaVise juniors (about $27 each) or, if they are too cheap to buy them, then some alligator-clip-based board holders for about $7 each.

Some students had enough time after soldering up their boards that I showed them how to get the frequency information that the KL25Z program was reporting to the SDA USB serial port (using the Arduino Serial Monitor).  Unfortunately, the old version of Windows running on the lab computers seems to have serious problems with cut-and-paste operations, and it was difficult to get more than a screenful of data that way.

Today was the last day of class, and I covered almost exactly what I proposed in last night’s blog post: one-transistor amplifiers, a review of the goals of the course, and getting suggestions for improvements for next year.

I briefly gave them an intro to NPN transistors (reinforcing the previous mention in the phototransistor lab), telling them that the collector current was basically β times the base-to-emitter current, and that the base-to-emitter junction was a diode.  The diode means that no current flows until the base-to-emitter voltage is at least 0.65V and that thereafter the current grows roughly with the square of the voltage above the threshold.

The first circuit I gave them was a common-emitter circuit with emitter degeneration:

Common emitter with emitter degeneration, which has gain of approximately –Rc/Re

I built the circuit outward from the transistor, first adding the two resistors for the base bias, to make sure that the base voltage was high enough to turn on the transistor, then the DC-blocking capacitor to remove whatever DC bias the input already has. I did not take the time to tell them that the RC time constant is .

I then asserted that and that (because β is large, so is a small fraction of the current).  But .  That means that the gain is .  I said that this design was good for providing high voltage gain, but was not good for providing high current (because is large).  I did not give them all the constraints on the components and signal levels needed to make sure that the amplifier works correctly.

I also gave them a common collector circuit:

This common collector circuit is good for high current gain, particularly if Rc is the load that current needs to be delivered to. I gave the example of a loudspeaker as the load.

The common-collector circuit is even easier to analyze: the emitter voltage follows the base voltage, but about 0.65v lower (hence the common name “emitter-follower” for this circuit), and the current is increased by up to about β.

I explained the difference between class-A, class-B, and class-C amplifiers by giving the clipping one would get on the common-collector amplifier as the DC bias of Vin got lower.  I pointed out that the class A amplifiers were always passing a wasted DC current, but that class-C were very efficient, being on for only a tiny part of the time.  I said that class C amplifiers were mainly used with LC tanks, and gave the analogy of a pendulum that you only gave a little tap at the end of each swing, to keep it swinging back and forth.

I then switched over to the review of the goals:

• Students passing BME 101L will be able to design simple amplifiers and RC filters for a variety of sensor-interfacing applications.
• Students passing BME 101L will be able to find and read data sheets for a number of analog electronics parts.
• Students passing BME 101L will be able to measure signals with multimeters, oscilloscopes, and data-acquisition devices,  plot the data, and fit non-linear models to the data.
• Students passing BME 101L will be able to write coherent design reports for electronics designs with block diagrams, schematics, and descriptions of design choices made.

Students were in agreement that these goals were mostly met, though they still felt a bit shaky on fitting non-linear models and were aware that there was a lot on the data sheets that they still didn’t understand. I confessed to them that I can’t read everything on most analog data sheets, but that the goal here was to get them to understand the basics of the data sheets (just some of the key parameters).  They felt that they’d gotten at least that far.  I will look into beefing up the presentations in the book and in class on fitting non-linear models, but I think they’re right that many of them have not really mastered that (though some are doing fairly well at it). I didn’t really ask them about their writing skills (an oversight on my part, not a deliberate omission). Many of them have improved their writing, though the average level is still not as high as I’d like to see.

I also checked on some of my subsidiary goals:

• to turn a few of the students into electronics hobbyists,
• to encourage a few to declare the bioelectronics concentration of bioengineering, and
• to teach some tool-using, maker skills (calipers, micrometer, soldering iron, …).

Somewhat surprisingly (and gratifyingly) about a third of the class now wanted to do electronics as a hobby—a topic they had mostly dreaded coming into the class. Only one was planning to the bioelectronics concentration, but a few said that if they were sophomores instead of seniors, they would have chosen bioelectronics. All felt that they had picked up a number of tool-using skills. Because there were a fair number interested in becoming hobbyists, I shared a number of company names that might be good for them to know about, giving a little information about each: Digikey, Mouser, Jameco, Sparkfun, Adafruit Industries, Itead Studio, Seeedstudio, Smart Prototyping, Elecrow, OSH Park, Pololu, Solarbotics, Santa Cruz Electronics, and Frys.  I forgot to mention Idea Fab Labs.

So on the matter of goals (major and minor), I think that the class was fairly successful, but there are still improvements to be made,  and I asked the class for suggestions. Here are a few of the main ones:

• oscilloscope training. The students did not feel that there was a usable tutorial or reference they could turn to on how to use the oscilloscope (and the Tektronix TDS3054 has pretty confusing controls).  I agree with them on this, and promised to write some material for the book to serve as a tutorial on using oscilloscopes.
• the sampling and aliasing lab in the first week didn’t mean much to most of them. Again, I agree, and I originally had that lab later in the quarter, after the students had done some work with time-varying signals. I had some difficulty packing all the labs into 10 weeks and having a report due each Friday—I didn’t want to split any 2-part labs over the weekend.  I’ll look into trying a rearrangement of the labs, but I’m not sure how to accomplish that.  Something to think about over the summer. It might be a good idea to talk about aliasing in some of the places where clipping is discussed, though they are rather different phenomena, sharing only the idea that the output data is not really what the input is about.
• students still felt uncertain of their ability to fit functions (like the power-law fit I asked for in one lab, but never gave them an example of).  I probably need to have some more worked examples in the book, and perhaps some exercises that are in prelabs rather than just in the final design reports.
• students did not identify any parts or tools that should be removed from the kits, but one suggested that tweezers be added (a good idea, though a finer tip pair of needle-nose pliers might be a better solution). Several felt that fume extractors should be added to the lab—I’ll talk to the lab staff about that for next year.

I also asked students about my idea of removing the soldering of the instrumentation amp board and soldering an audio premap board as well, so that the power amp lab could go faster (and that we could have them test single-transistor class A amplifiers before building the class D amplifier). The students were a bit dubious about this idea, but I think I might try it next year anyway.

Students were more enthusiastic about the idea of my writing variants of each lab to perform at home, without the expensive equipment of the lab.  I’ll try to do that this summer, maybe writing up three versions of some labs: one using only the KL25Z board and a cheap ($10) multimeter, one using those plus a USB oscilloscope (like my Bitscope oscilloscope), and one using the suite of expensive equipment in the lab.  I think that some of the labs will be very challenging with cheap equipment and others will be straightforward.

The loss of the good oscilloscope will probably be most limiting, though with a decent laptop the PteroDAQ data acquisition software can run with a sampling rate of 600Hz for a single channel (the limitation seems to be the program on the laptop keeping up with the USB input so as not to lose a byte and get out of sync).  The old Windows boxes in the lab start dropping bytes even at a 100Hz sampling frequency, but I can go up to 600Hz (but not 650Hz) for a single channel on my MacBook Pro. A newer laptop could probably keep up with a 1kHz sampling rate.  We can do a lot even with the low sampling rate, but it is nice to see somewhat faster signals (like the rise and fall times of the FETs in the power amp lab).

A USB oscilloscope like the Bitscope B10 should be enough for just about all the labs in the course, though I will have to look into how well it does with looking at the rise and fall of the FET gates and drains (without slowing down the waveforms: see Last power-amp lecture for  Bitscope recording of slowed-down transitions and Power amps working for Tektronix images of full-speed transitions). (I did a cursory check tonight, and it looks like even with subsampling it is difficult to get a good view of the gate signal with the Miller plateaus with the Bitscope unless I slow the transitions down.)

My old Fluke 8060A multimeter seems to have died this spring, so I’ll see how much I can do with super cheap hardware-store multimeters.  I think that the impedance characterization of the loudspeaker and electrodes will be the hardest to deal with, but some careful attention to the input impedance of the voltmeter may make even those labs feasible. I’ll probably have to limit the frequency range and use two cheap meters (which I have, and my son has yet another cheap multimeter that I could borrow this summer).

I did mention to the students my idea (borrowed from UCSB) of having students buy their own oscilloscope and voltmeter probes, rather than having to contend with locked down probes that can’t reach the bench or probes broken or stolen by other students. They were lukewarm to the idea—neither endorsing nor embracing it. They’d probably like a cheaper solution, but I don’t know of one as long as EE lets their students into the labs unsupervised (something else I’m trying to get changed, as the EE students do not seem to be willing to follow even simple safety rules, like not bringing open cups of tea and coffee into the lab).

I got a little less than half my grading done this weekend (all the lab reports for the final lab, but not the redone reports from earlier labs, and not the 2–3 senior theses that had to be redone from last quarter) before I burned out.  I decided to do a little playing with my Bitscope USB oscilloscope, as a break from grading, and that sucked me in—I still haven’t gotten back to the grading.

Here is the problem I was addressing: In my book draft and in my blog post Third power-amp lecture and first half of lab, I presented a view of the Miller plateaus of an nFET, obtained by slowing down the transitions with series resistors and added gate-source capacitance, recording the result with my Bitscope USB oscilloscope, and averaging many traces together.

Here are the gate and drain voltages for an AOI518 nFET, slowed down by adding a series resistor to the gate signal and a large capacitor between the gate and drain. I slowed it down so that I could record on my low-speed BitScope USB oscilloscope—students can see high-speed traces on the digital oscilloscopes in the lab. The Miller plateaus are the almost flat spots on the gate voltage that arise from the negative feedback of the drain-voltage current back through the gate-drain capacitance.

I was rather unsatisfied with this approach, as I really want to show the full-speed transitions. In Power amps working, I showed some Tektronix plots, but their little screen images are terrible (as bad as the Bitscope screen images), and I can’t use them in the book.

With an 8Ω loudspeaker as a load, turning off the nFET (gate voltage in blue) causes a large inductive spike on the drain (yellow).

What is the fascination that scope designers have with black backgrounds? I know that the traditional cathode-ray-tube scopes gave no other choice, but for digital scopes black backgrounds are just evil —they don’t project well in lectures and they don’t print well on paper. It would be possible for me to use the data recording features of the Tektronix scopes, and plot the data using gnuplot, but I’d rather use the Bitscope at home if I can (much less hassle than transporting everything up the hill to the lab every time I need some more data).

The Bitscope B10 is capable of 20Msamples/s, which should give me decent time resolution, but the discretization noise is pretty large, so I want to average  multiple traces to reduce the noise. When using the “DDR” (DSO Data Recorder) option of the BitScope, it becomes very clear that they do not have any software engineers working for them (or didn’t at the time they defined the format for the recorder files).

The files are comma-separated values files, with no documentation (that I could find) of their content except the first line:

trigger,stamp,channel,index,type,delay,factor,rate,count,data

Each row of the file after that seems to have one trigger event, serially numbered in the first field, with a low-resolution time-stamp in the second field (hh:mm:ss, but no date and no finer time divisions).  The channel is 0 or 1, the index increments serially separately in each channel, the type is always 0, the delay is when the trace starts relative to the trigger (in seconds), the factor is always 1, the rate is the sampling rate (in Hz), the count is the number of data points, and the data is not a single field but “count” more fields. There is no other meta-data about the settings of the scope!

The data, unfortunately, is not the voltage measured by the scope, which is what one would naively expect.  Instead, you have to divide by the volts_per_division and add the offset voltage—neither of which are recorded anywhere in the data file! (You probably have to adjust for the probe as well, but I was using a 1X probe, so I can’t tell from this data.)

It is clear that the “engineers” who designed this format never heard of metadata—maybe they were used to just scrawling things on the backs of envelopes rather than keeping data around.  Yes, Bitscope designers, I am publicly shaming you—I like the Bitscope hardware well enough, but you are clearly clueless about data files! A correct format for the data would have had a block at the beginning of the file recording every setting of the scope and the full date and time, so that the precise conditions under which the data were recorded could be determined and used. (For example, was the RF filter on or off? what were the trigger conditions?)

I was able to read the DDR csv file and extract the data, but I found a number of other apparently undocumented properties of the B10.  If I switched away from post-trigger recording to having the trigger 25% or 50% of the way through the recording, the maximum sampling rate drops by a factor of 3 to 6.7MHz, so I need to use POST triggering, in which the recording starts about 1.25µs after the trigger. I can delay the part of the data I look at (only the part on the screen is saved), but if I delay too much, the sampling rate drops back down again.

One big problem is that the jitter on the Bitscope trigger is enormous—up to 150ns, which is 3 samples at the highest sampling rate. The image bounces around on the screen, and the data recorded in the files is similarly poorly aligned.

If I average a bunch of traces together, everything smooths out.  Not just the noise, but the signal as well! It is like passing the signal through a low-pass filter, which rather defeats the purpose of having a high sampling rate and averaging traces.

So today I wrote a program to do my own software triggering in a repetitive waveform. I recorded a bunch of traces that had the waveform I was interested in—making sure that the RF filter was off and the waveform was being sampled at the highest sampling rate. The program that read the csv file then looked in each trace for a new trigger event, interpolating between samples to get the trigger to much higher than single-sample resolution (by triggering on a fast rise, I can get about 0.1 sample resolution). I then resampled the recorded data (with 5-fold oversampling) with the resampling synchronized to the new trigger.  The resampled traces were then averaged.

Here is an example of the Vgs voltage of an nFET transistor being driven by an S9013 NPN transistor and a 270Ω pullup (the NPN  base was driven by the square wave from my Elenco FG500 function generator, through a 2kΩ resistor). The drain of the nFET had an 8Ω loudspeaker to a 5V USB power line.

The two traces on the right show a single trace (red) and an average of all the traces (magenta). Both of these are aligned by the Bitscope trigger event, which was substantially before the recording (much more than the minimum 1.25µs, as I’d deliberately delayed to get the next pulse).
The left-hand trace is also an average, but after retriggering on the first rising edge at 0.2v.
Note that the jitter in the trigger (and in the signal source) caused enormous rounding of the magenta curve, but retriggering to better than 5ns resolution allows the signals to be properly averaged.

The averaged plot is probably usable in the textbook. I also tried averaging the same traces triggering on the falling edge, to see if that got any more clarity for the ringing when the nFET is turned off, but it ended up looking essentially the same. On my Kikusui 60MHz analog scope, I see the little ripples after the downward transition (a 10MHz damped ripple), but I don’t see the hump in base line visible in the Bitscope trace.  I think that hump may be an artifact of taking too much power from the 5V USB line powering the Bitscope (or of coupling back of the inductive spike).

I tried putting in an LC filter on the 5V power line from the Bitscope (a 470µF capacitor to ground, a 200mH inductor, and another 470µF capacitor to ground).  This seems to have cleaned up the problem (this was hours later, and the frequency of the generator was almost certainly different, as I’d played with the tuning potentiometer several times):

Keeping the power supply noise from propagating back to the Bitscope cleans up the signal considerably. The 10MHz ripple is now clearly visible. I tried zooming in with gnuplot and the resolution looks as good as on my 60MHz analog scope. The dejittering and averaging has made for a very fine signal.

One problem with this retriggering approach is that it doesn’t really work with two channels—the Bitscope traces for the two channels are separate events, and the only synchronization information is the hardware trigger. I could get a clean Vgs signal and a clean Vds signal, but aligning them is not going to be any better than the jitter of the hardware trigger. I’ll have to think about averaging (or taking the median) of the trigger times relative to the hardware trigger, and using that to align the two traces.

Still, I wonder why the Bitscope designers have not taken advantage of the trigger jitter to do averages of repetitive traces—it allows one to reconstruct signals in software that are much higher bandwidth than the sampling rate of the scope.  These sorts of super-resolution techniques are pretty common, and it only requires better software, not new hardware.

I’ve been thinking that I might even try writing some software that talks directly to the Bitscope hardware (they have published their communication protocol), so that I can do things like capturing the data with full metadata and looking at it with decent plotting software (Matplotlib or gnuplot).  I’m not into doing GUI programming (an infinite time sink), so I’d probably write a Python library providing a application program interface to the Bitscope and a number of simple single-use programs (like capturing and averaging waveforms) with a configuration file or command-line arguments to set the parameters. Yet another thing to add to my to-do list (but near the end—there are many more important things to work on).

In Bitscope jitter and nFET Miller plateau,  I gave a nice super-resolution plot of the gate voltage on an nFET using the Bitscope and subsequent dejittering of the trigger:

Here is an example of the Vgs voltage of an nFET transistor being driven by an S9013 NPN transistor and a 270Ω pullup (the NPN  base was driven by the square wave from my Elenco FG500 function generator, through a 2kΩ resistor). The drain of the nFET had an 8Ω loudspeaker to a 5V USB power line.

Keeping the power supply noise from propagating back to the Bitscope cleans up the signal considerably. The 10MHz ripple is now clearly visible. I tried zooming in with gnuplot and the resolution looks as good as on my 60MHz analog scope. The dejittering and averaging has made for a very fine signal.

But I didn’t give the schematic for the test jig.  So here it is:

Test jig for creating the Miller-plateau plot.

Something else I didn’t point out in the previous post: the quantization error is still visible in the slow-moving parts of the signal (at the beginning and near the top of the gate charging), but is essentially eliminated in fast-changing portions of the signal.  I think that the dejittering and averaging gets good values if the jitter is large enough to move the signal to value that would have a different quantized output, so we are averaging values that are sometimes too high and sometimes too low. But if the jitter doesn’t move the signal that far, then we’re relying entirely on voltage noise to change the quantized output and get averaged out, and the voltage noise seems to be much smaller than the step size of the analog-to-digital converter.

For the book, I might redo the plot using a comparator to drive the nFET, rather than the S9013 NPN transistor, though there is some advantage to leaving the comparator out of the picture, so that students will have to think a bit about their own design, rather than simply copying.

I might want to try slowing down the falling edge, so that Miller plateau is visible on both edges. I could slow down the fall by increasing the size of R2 (reducing the base current from 1.2mA and hence the collector current).  I could probably reduce the base current to 200µA and still switch the nFET off, since with a typical current gain of about 120 for the S9103, I should still be able to get a collector current of about 24mA, which is more than 5V/270Ω=18.5mA.  Even 100µA may be enough, but then the low voltage on the nFET gate may start creeping up, and we don’t want to leave the nFET partially on. (The same reasoning argues against adding a series resistor between the collector and the gate.)

The current through the S9013 seems to be much larger than available from the LM2903—maybe I should do current vs. voltage (Ic vs Vce) plots for the S9013 with various base-emitter currents, though the data sheet already has a nice plot of that.

I should probably also try using a resistor rather than a loudspeaker as a load, though the inductance of the speaker is helping to limit the current and avoid overloading the USB power supply.  With a simple 10Ω resistor,  I’d be getting 500mA, which is the USB limit. With the inductive load of the loudspeaker, the current builds up slowly when the nFET is on, and never gets close to what we’d expect from the nominal 8Ω value.

Another thing I might do is to use a hysteresis oscillator to drive the NPN transistor.  That would be more in keeping with the minimal-equipment approach I’m going to try to add to the book this summer.  (I might also play with a larger voltage for the loudspeaker, since that should give a larger swing on the drain voltage, and hence a clearer Miller plateau.)

In Bitscope jitter and nFET Miller plateau and Update for nFET Miller plateau I talked about using the Bitscope BS10 USB oscilloscope and post-processing to remove the trigger jitter to get a better trace of the Miller plateau when switching an AOI518 nFET.  I wasn’t entirely happy with that result, as I was using an external function generator (albeit a cheap Elenco FG500 box that puts out rather poor waveforms).  I thought I could do as well or better using a hysteresis oscillator to generate the square waves.

So I came up with the following circuit:

Test fixture for looking at the Miller plateau on the AOI518 nFET.

The top-left section, with the capacitors and the big inductor are just to keep the power supply clean. Because the power is coming from the 5V USB supply, passed through the Bitscope, any noise coupled back through the power supply can affect the readings, so I made sure that no high-frequency noise would be coupled back to the Bitscope that way.  One 4.7µF bypass capacitor (C6) is right next to the 74HC19N Vcc power pin on the breadboard and the other (C5) next to the emitter of the S9013 NPN transistor.  These helped in reducing ringing on the transitions of the square wave.

The Schmitt trigger U1 is the relaxation oscillator that oscillates at about 550kHz, and U2 buffers the output so that the load on the oscillator is constant.  R2 and C4 couple the output of the oscillator to the base of the NPN transistor Q2, which is configured as a common-emitter amplifier.

When Q2 is turned on, it sinks about 18.5mA of current (5V/270Ω), which at the nominal current gain of 120 for S9013 transistors, means about 150µA of base current. When Q2 is turned on it initially sinks even more current, discharging the gate  Q1 fast, but when Q2 is turned off, the gate is pulled up more gradually by the 270Ω resistor R1.  This gradual rise of the nFET gate voltage allows us to observe the Miller plateau when the nFET actually switches on.

The common-emitter amplifier using Q2 can switch very rapidly with no load, but adding the gate capacitance of Q1 makes the rise follow an RC charging curve. If the 150Ω load resistor R4 is omitted, the curve is smooth, as there is no voltage swing on the drain. Putting in R4 results in the drain voltage dropping rapidly when Q1 turns on, which is coupled back to the gate through the Miller capacitance, resulting in the Miller plateau.
These traces were gathered and dejittered separately (each is the average of over 500 traces). The time alignment was done by hand, and may not be completely accurate.

The initial rise in the drain voltage (from about -0.9 to -0.7 µs in the plot) is due to capacitive coupling of the rising gate voltage to the drain with the nFET off, and there is a similar overshoot at the lower end as the nFET is turned off (just before 0µs).

I played around quite a bit with the bias network R2 and C4 for the base of Q2. The resistor alone doesn’t work, as the base voltage remains a constant 340mV and the NPN transistor remains always on—I was a little confused by this, as the 340mV measurement on the Bitscope seemed too low to turn on an NPN transistor. I think that there is a calibration error on the Bitscope—according to my Kikusui COS5060 analog oscilloscope, the high voltage is about 600mV, which seems to be a more reasonable Vbe for a transistor that is on.

It seems that the offset that the Bitscope BS10 provides is inaccurate: I get a reading of 740mV for an offset of 2V, 1V, or 0V; 500mV with an offset of -1V; and 320mV with an offset of -2V or -3V.  Looking at the ground line with the same channel also shows an error for the -1V, -2V, -3V and -4V offsets (on the 11V range): -300mV for -1V, -560mV for -2V, -3V, and -4V. But those offsets are different from the ones I’m seeing with the oscillating base signal, so I suspect that it isn’t even a simple offset error.  This is bad—I’m going to have a hard time correcting such large and varying errors. I should probably ask the Bitscope technical staff whether large errors in the offsets are normal, or I have a damaged Bitscope BS10.  They’ve not made the schematic available, so I’m not sure what they are doing internally to provide the offset voltages.

The capacitor C4 alone also doesn’t work to bias the base, as the voltage on the base then doesn’t get high enough for  the NPN transistor to  turn on. With both the resistor R2 and the capacitor C4, the base swings about 5V, with the high value being the Vbe where the NPN transistor turns on. The resistor value is not critical—reducing R2 to 2kΩ moves the bottom end of the swing up a little, but seems to work just as well.  A very large resistor (100kΩ) seems to result in slow turn on for Q1.

The effect of changing C4 was not something I would have predicted—as I lower C4 (raising the corner frequency of the high-pass), I get a lot more ringing of the gate voltage, but faster transitions as well. I think that the faster transitions come from the base voltage not dropping as far below threshold when Q2 is off, so that it can rise above threshold sooner when Q2 needs to be turned on.

Smaller capacitors for C4 result in faster edges when turning on the NPN transistor, with more overshoot and ringing. Once the capacitance is large enough, there is little further change.

The curves above were synchronized by the setting 0µs at the upward transition past 4.0V, which seems to overlay the dejittered waveforms fairly well. Over 900 traces were averaged for each of the 5 curves.

I could also provide a DC bias current for Q2 by removing R2 and connecting the base via a 10kΩ resistor to the clean +5V supply. That seems to work just as well, but moves up the lower end of the base voltage swing, which may result in slightly faster turn-on of the NPN transistor.

It’s nice that I can use the Bitscope (with dejittering) to produce the Miller plateau figure for the textbook, but I’m concerned about the erroneous offsets on the Bitscope.  I’m wondering what else I’ve been relying on that is miscalibrated.